An n-be is a shape formed from an n-cube by the removal of half of each cube in such a way that at least half of the original join between cubes is retained. The diagram below shows the one monobe; the three dibes; and the seventeen tribes.
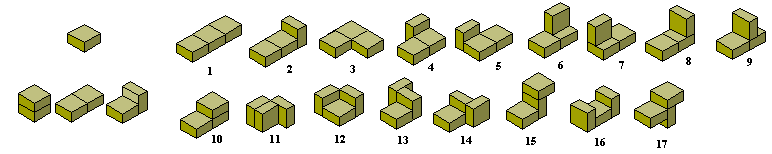
Brendan Owen has found the number of polybes up the hexabes as shown in the table below.
The 17 tribes together make a volume of 25½ cubic units. This is three half cubes short of a 3x3x3 cube and a number of constructions are possible for fitting the 17 pieces into a 3x3x3 cube. One is shown below.
A great many constructions are possible with the 17 tribes. The diagrams below show a number of solid shapes made up of 25½ cubic units. Marek Ctrnact has found solutions to all of these using Peter Esser's solver. Click on the image for the solutions.
The solid below consists of a 1x5x5 block with a single half block in the centre of a 5x5 face. A solution of this problem is shown below and constructions with the half cube in other positions on the face are possible. There are in fact 20 different possibilities for the position of the half cube (see lower diagrams). The half cube could also be placed on the side of the block giving another 6 problems.