
Various sites also give a variety of more esoteric polyforms. Use the links below to find them.

Jacques Ferroul has produced a number of other poyforrm sets. These are described on his site.
![]()

Various sites also give a variety of more esoteric polyforms. Use the links below to find them.

Jacques Ferroul has produced a number of other poyforrm sets. These are described on his site.
![]()
Various different types of polyforms have been suggested and studied and a variety of these is discussed in this page. Because, in order to produce a polyform, it is usually necessary to start with one of the three regular tiling patterns (squares, equilateral triangles or hexagons) most of these are either subsets or derivations of the main polyforms - polyominoes, polyiamonds and polyhexes. Some of these and others are discussed in Miroslav Vicher's site. Kate Jones' Rhombiominoes are also in this category (more information on these is available at Pentomino hungarIQa where they seem to have been rediscovered). Brendan Owen has made two 6x31 parallelogram with the 62 pieces made with six rhombi.
It is possible to make simultaneous pentuplications and sextuplications of pieces with the piece replicated being omitted.
It is also possible to make simultaneous two-, three- and sevenfold copies of a piece.
1. Polyforms derived from combinations of other n-forms.
There is a variety of polyforms of this type and most of the information known can be seen on a separate page.
2. Polyforms derived from the division of n-forms.The polyforms produces by dividing squares, hexagons and cubes are on separate pages in this site (see polyares, polyhes and polybes).
If we try dividing each triangle of a polyiamond in two then we tend to get some very complex pieces but if we include the restriction that each cut be the same on both sides of a join then we produce pieces such as those below derived from the tetriamonds, pentiamonds and hexiamonds.
Whether anything reasonable can be constructed from these pieces seems unlikely. Also the number of pieces is very small and does not increase significantly as we go to higher order polyiamonds.
The polyforms derived from joining half equilateral triangles together have been studied quite extensively. These are usually known as polydrafters or polydudes. Information on these can be found at Miroslav Vicher's site and Ed Pegg Jr.'s Mathpuzzle.com. As an example of the difficulty of constructions with these shapes Patrick Hamlyn took 830 hours of computer time to find two solutions to the problem below with pieces made up of 9 half equilateral triangles.
3. Polyforms derived from the removal of half of one of the basic tiling shapes.
A great deal of work has been done of polyforms of this type and most of the information known can be seen here.
Miroslav Vicher has introduced the concept of strip polyforms which are subsets of the standard polyforms. A strip polyform is a singly connected set of squares. As an example of these sets below is shown some constructions with the 13 strip-hexominoes and a variety of rectangles made with the 30 strip-heptominoes. The figure at the top right shows a 9x10 rectangle with 12 internal holes.
Patrick Hamlyn has found an 8x64 rectangle made with the 64 strip octominoes. Also shown here are Patrick's three solutions of a pair of side 16 squares made with the set.
A subset of the strip polyominoes is the staircase polyominoes or polysnakes which can be defined as a minimal set of squares connecting one corner of a rectangle to the opposite one. Brenadan Owen has some data on these in his site. The size 6 and 7 sets are shown here.
The next two diagrams show the 5 strip-hexiamonds and the 8 strip-heptiamonds and the 6 and 7 strip-polytans. The strip polytans are assumed to have no two pieces forming a square but none of these sets has an even number of pieces and so each construction has one piece left over. The strip-pentatans where two pieces forming a square are allowed are shown at the right below. Again no rectangles are possible.
There are ten strip pentahexes and fifteen one-sided strip pentahexes.
We can also look a strip polycubes. The are 16 strip pentacubes which can make 4x4x5, 2x4x10 and 2x5x8 boxes.
If we consider one sided polystrips then the strip pentominoes can form a 5x10 rectange as well as some other figures including a 6x9 rectangle with a hole in the shape of a tetromino.
With the one-sided strip hexominoes there are 24 pieces which can make a number of rectangles. The only other rectangle which might have been possible is a 4x36 which cannot be made.Similar hole constructions are also possible as shown at the bottom of the figure below.
5. Polyforms derived from non-regular tessellations
Examples of these possibilities are shown below. Little or nothing has been done in this area but Livio Zucca has some information.
If we use the grid below then we obtain sets of shapes which we could call polypons from the isosceles triangle (pons asinorum) which is the basis of the tessellation.
If we restrict the sets so that no 30º angle is produced then we get the following sets of what we may call blunt polypons and it seems likely that higher order sets could produce some interesting constructions although the numbers grow very slowly (see right hand column of the table above). The 13 enneapons have an area equal to that of a 5-3 trapezium and the 102 dodecapons could well have formed a number of parallelograms and trapezia except for the fact that one of the pieces has a 330º angle which cannot be filled and so perhaps for this and higher sets we should add the stipulation that no 330º angle is produced either. If we omit the dodecapon which is in the shape of a triangle then the remaining 100 pieces could well form a triangle.
Brendan Owen has calculated the number of polypons for n = 1 to 20 and has produced images for n up to 12. Click on a yellow rectangle to see images of the set.

The star below made with the ten hexapons has a unique solution.
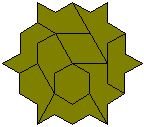
If we reduce the restriction of the pieces to fit into the above grid and allow combinations of pons in a triangular grid then we get extra pieces as shown below. The only known symmetric construction with the tetrapons is shown together with two construction in which one piece is used twice.
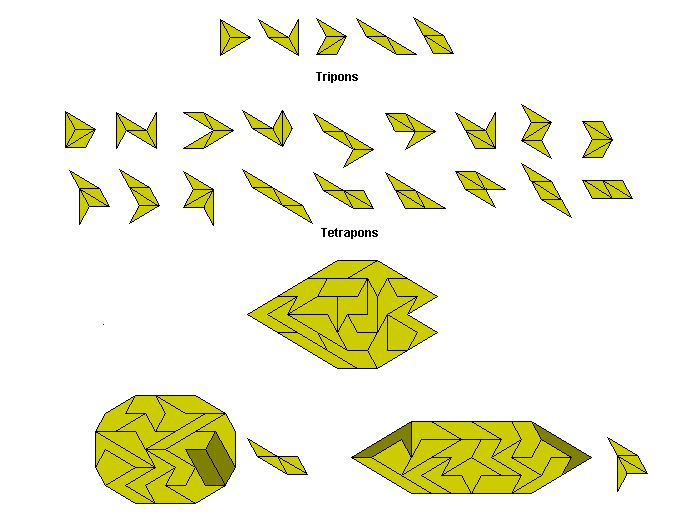
The numbers of pieces in this case are as below.

Brendan Owen has also made the hexagon below based on a set of pieces made up of four adjacent sections of the grid at the left. Notice that using this grid we get some shapes that are the same but can be made in different ways as, for example, the two shapes at the right.
Brendan has also used this set to make scale models of the seven tetrahexes.
The hexagon above is a sixfold replica of an hexiamond and Brendan has produce the following pairs of figures which can be used to make replicas of all twelve hexiamonds.
We can define the diameter of a polyiamond as the smallest triangle into which the polyiamond will fit. Under this definition there are 17 diameter 3 polyiamonds which have a total area of 104 unit triangles. These pieces are shown below as well as a number of constructions made with them.
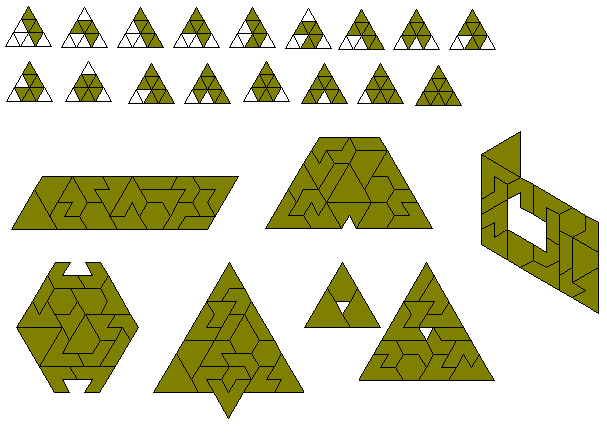
If we look at the one-sided set we have 24 pieces covering an area of 143 triangles.