An n-are is a shape formed from an n-omino by
the removal of half of each square in such a way that at least half of the original
join between squares is retained. Brendan Owen has supplied the following table
of numbers.
The disgram below illustrates how the triares are formed from
the three tominoes.

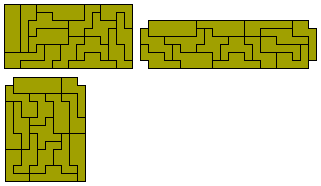
The 9 triares formed from the two trominoes
Below are six constructions made with this set of pieces. The
only rectangle possible is the 6x9 shown. There are a number of solutions to
a 5x11 rectangle with a single hole. This hole cannot be at the centre of the
rectangle because of colouring considerations. The constructions at the right
are triplications of two of the pieces. It is likely that the other triplications
are not possible.
The triares can also form a 6x10 rectangle with a hole in the
shape of one of the 24 balanced hexominoes.The diagram also shows some solutions
for 5x12 and 4x15 rectangles.
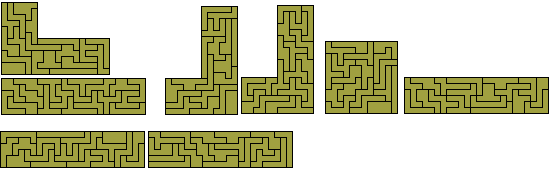
The 42 tetrares cover a total area of 84 full squares and could
therefore cover rectangles 2x42, 3x28, 3½x24, 4x21, 6x14, 7x12, 8x10½. The 2x42
is not possible as can be seen from the fact that at least one of the pieces
(below) must divide the rectangle into parts whose areas are not multiples of
two unit squares.
The diagram below shows two 3x14 rectangles and two 4x10½ rectangles
which can combine to form the 3x28, 4x21, 6x14, and 8x10½ rectangles. The two
3½ x12 rectangles by Roel Huismann give 3½x24 and 7x12.


There is also a number of other constructions
which could be possible with the set in particular the similar hole solutions
below..
The tetrares can be sextuplicated using 36 of the 42 pieces.
The sets of constructions below can make sixfold copies of 33 of the 42 pieces.

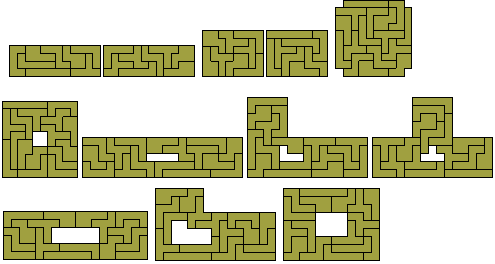
Pentares
There are 180
pentares including
two pieces with holes. My thanks to Brendan Owen for checking the number of
pentares and for providing a diagram of the
hexares.
If we consider mirror images as distinct there are 16 triares
with a total area of 96 units. With this set 4x24, 6x16 and 8x12 rectangles
are all possible as shown below where there are two 4x12 rectangles made and
two 6x8 rectangles from the set. Also included are two constructions based on
a 10x10 square and some similar hole solutions.
The two 4x12 rectangles also provide a solution to the problem
of quaruplication for two of the pieces. All quadruplications are possible.
The remainder are shown below.
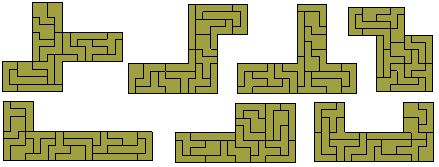
There are 77 one-sided tetrares which can form at least one
rectangle.
The three polyares with perimeter 6 are shown below together
with the five one-sided pieces.
With perimeter 7 we get nine pieces with a total area of 14½.
These cannot make a rectangle but if we use one of the seven pieces with area
1½ twice then we might be able to make a 4x4 square. Five of these problems
can be solved and it seems unlikely that the other two are possible. Some constructions
made with the full set are also shown below.
The one-sided perimeter 7 set consists of 15 pieces.
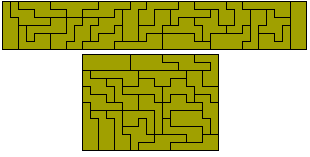
There are fifteen polyares with perimeter 8 with a total area
of 32 unit squares shown here in the only possible rectangle - 4x8.
The one-sided set consists of 27 pieces with a total area
of 57. There are two possible rectangles with this set - 3x19 and 6x9½ as
shown below.
.

There are thirty nine perimeter 9 polyares with a
total area of 84 unit squares. This is the same area as the tetrares and
so it may well form the same rectangles - 3x28, 3½x24, 4x21, 6x14, 7x12,
8x10½. The 3½x24 and 4x21 are shown below .
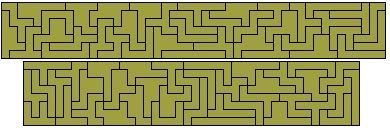
The one-sided set consists of 75 pieces with a total area of 162 unit squares.