 |
 |
 |
 |
 |
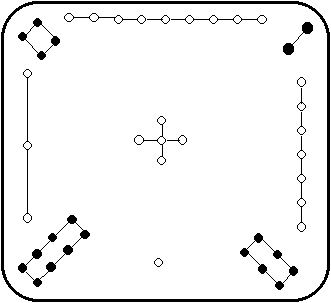 A 3 x 3 magic Square dating
back to about 2850 B.C. It is attributed to Fuh-Hi, the mythical founder of Chinese
civilization, who lived from 2858- 2738 B.C.
A 3 x 3 magic Square dating
back to about 2850 B.C. It is attributed to Fuh-Hi, the mythical founder of Chinese
civilization, who lived from 2858- 2738 B.C.
The odd numbers are expressed by white dots, i.e. yang symbols, the emblem of heaven.
The even numbers are represented by black dots, the yin symbol, the emblem of earth.
This is the oldest known example of a magic square. It is also the only possible arrangement of the first 9 numbers into a magic square (not counting the 3 rotations and 4 reflections).
![]()
12 Magic Circles - 6 Magic Squares
This array contains six 4 x 4 pan-diagonal magic squares which each sum to 194 in 52
different ways.
(4 rows, 4 columns, 2 main diagonals, 6 broken diagonal pairs, corners of 4 - 3 x 3
squares, corners of 16 - 4 x 4 squares including wrap-around, and 16 - 2 x 2 squares
including wrap-around.)
The twelve circles of 16 numbers each sum to 776 ( 4 times 194).
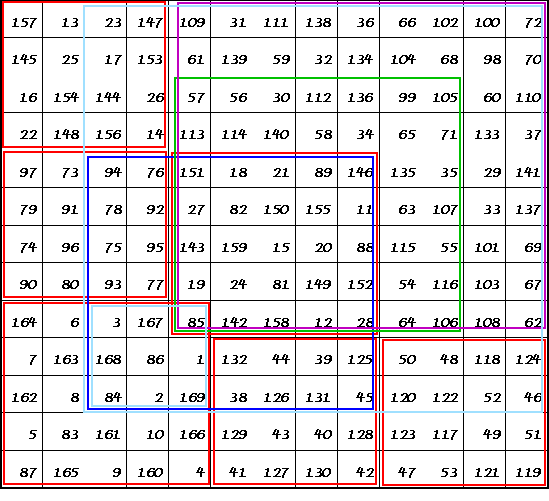
E 4 x 4 magic square as D.
F 9 x 9 magic squares. All rows, columns, & the 2 main diagonals =
765.
G 5 x 5 magic square as C.
H 9 x 9 magic square as F.
I 7 x 7 magic square. All rows, columns, & the 2 main diagonals =
595.
J 13 x 13 magic square. All rows, columns, & the 2 main diagonals =
1105.
K 11 x 11 magic square. All rows, columns, & the 2 main diagonals =
935.
L 7 x 7 magic square as I.
M 3 x 3 semi-magic square. All rows, columns, but only 1 main diagonal =
255.
All 169 cells in this array are included in at least two different magic squares. The cell containing the number 85 appears in six different magic squares. It is also in the correct diagonal of the 3 x 3 semimagic square!
This array was invented by L.S.Frierson and appears in Magic Squares & Cubes by W.S. Andrews, publ. in 1917.
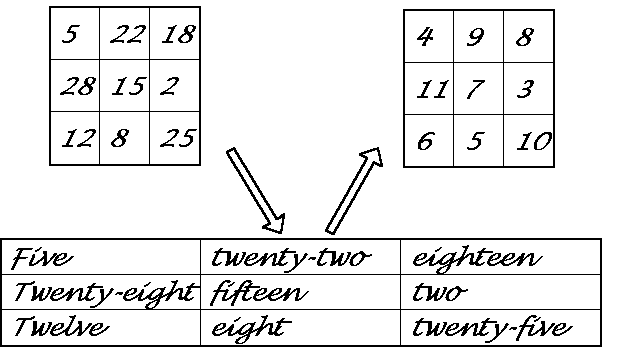
Spell out the numbers in the first magic square. Then count the letters in these number words. The integers make a second magic square. This second square contains the consecutive digits from 3 to 11. This first square is referred to as an 'alphamagic' square. It was invented by Lee Sallows who made a thorough investigation of this type of square and reported the results in Abacus (1986 & 1987). It has since appeared in many publications.
Sign of the Beast
Add 100 to each cell of the above two magic squares. Now add the corresponding cells
together to make a new magic square. The constant of this new square is 666.
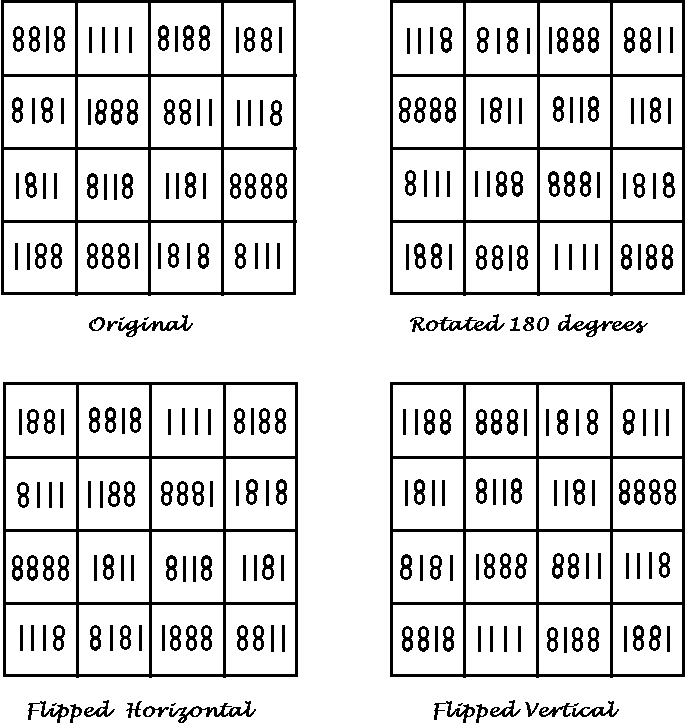
This novelty magic square is known as the IXOHOXI magic square. It is magic in all four of the above orientations. It is pan-diagonal so 4 rows, 4 columns, 2 main diagonals, 6 complementary diagonal pairs and 16 2 x 2 squares all sum to 19998.
Check this out with a mirror! All numbers in the reflection will read correct because both the one and the eight are symmetric about both the horizontal and the vertical axis. Note also that the name IXOHOXI has the same characteristics.
![]()
Upside-down magic square
 The following digits are correct if rotated 180 degrees
The following digits are correct if rotated 180 degrees
i.e. 0, 1, 6, 8, 9 when rotated 180 degrees becomes
6, 8, 9, 1, 0.This magic square is still magic when rotated 180 degrees
However, if these digits are simply turned upside down the 6 becomes a
backward 9 and the 9 a backward 6.
If you turn the square upside down, then reverse the 6’s and 9’s so they
read correctly, you end up with different numbers, but the square is still magic!
Notice that corners of any 2x2, 3x3 or 4x4 squares also sum to 264, as well as many other combinations.
| 1 | 143 | 142 | 4 | 5 | 139 | 138 | 8 | 9 | 135 | 134 | 12 |
| 13 | 23 | 121 | 120 | 119 | 27 | 29 | 31 | 113 | 112 | 30 | 132 |
| 131 | 117 | 41 | 103 | 102 | 44 | 45 | 99 | 98 | 48 | 28 | 14 |
| 130 | 105 | 96 | 55 | 89 | 88 | 59 | 84 | 60 | 49 | 40 | 15 |
| 129 | 39 | 95 | 87 | 65 | 79 | 78 | 68 | 58 | 50 | 106 | 16 |
| 128 | 107 | 51 | 62 | 76 | 70 | 71 | 73 | 83 | 94 | 38 | 17 |
| 18 | 37 | 93 | 82 | 72 | 74 | 75 | 69 | 63 | 52 | 108 | 127 |
| 19 | 36 | 53 | 64 | 77 | 67 | 66 | 80 | 81 | 92 | 109 | 126 |
| 125 | 35 | 54 | 85 | 56 | 57 | 86 | 61 | 90 | 91 | 110 | 20 |
| 21 | 111 | 97 | 42 | 43 | 101 | 100 | 46 | 47 | 104 | 34 | 124 |
| 22 | 115 | 24 | 25 | 26 | 118 | 116 | 114 | 32 | 33 | 122 | 123 |
| 133 | 2 | 3 | 141 | 140 | 6 | 7 | 137 | 136 | 10 | 11 | 144 |
All these squares are magic in all rows, all columns, and 2 main diagonals.
Magic sums: Order-4, 290; Order-6, 435; Order-8, 580; Order-10, 725; Order-12, 870.
The order-12 is a pure magic square, i.e. it contains the consecutive integers 1 to 144
(122).
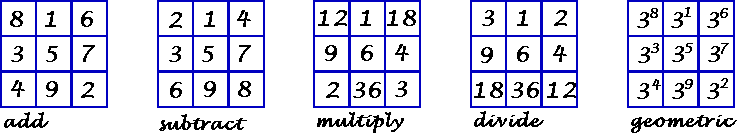
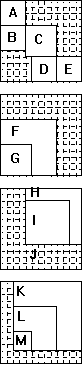
| Add | The normal order 3 magic square. This is the only basic
solution for the order-3. The constant is 15. |
| Subtract | Constructed by interchanging the contents of diagonal opposite corners. Now, if you add the two outside numbers and subtract the center one from the sum, you get the constant 5. |
| Multiply | Constructed in the same sequence as the normal order 3 m.s. Start each sequence of 3 integers by doubling the value of the previous sequence start number. The 2nd number in the sequence is 3 times the 1st number. The 3rd number in the sequence is 3 times the 2nd number.. Multiply the 3 numbers in each of the eight lines to obtain the constant 216. |
| Divide | Construct the same as the multiply m.s., then interchange diagonal opposite corners. Now, by multiplying the outside numbers of each line, and dividing by the middle number, the constant 6 is obtained. |
| Geometric | Raise the number in each cell by the power indicated. The product of the 3 numbers in each row, column, or diagonal will be the magic constant, in this case 14,348,907. Or, for a short cut, raise the number to the sum of the powers in each cell of the line. NOTE that the exponents are arranged the same as in the normal magic square. This works for any base number. |
![]()
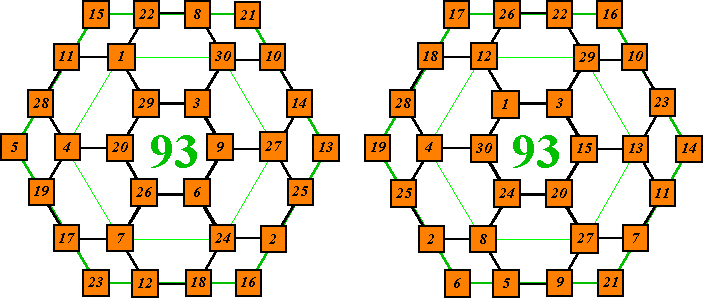
Numbers 1 to 30 arranged so that the corners of each of the nine
hexagons sums to 93.
Two of many solutions.
![]()
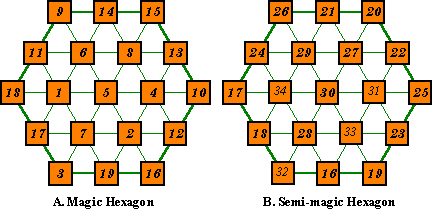
"A" shows the unique solution for this arrangement of the integers 1 to 19. The 6 lines of 3 numbers; 6 lines of 4 numbers; and 3 lines of 5 numbers each sum to 38.
No other solution for any order hexagon is possible !!
"B" is formed by picking an arbitrary number, in this case 35, and subtracting each number in "A" from it. This arrangement has the characteristic that each of the 6 lines of 3 integers sum the same, in this case 67. Each of the 6 lines of 4 integers sum to the same value, in this case 102. And each of the 3 lines of 5 integers sum the same, in this example, 137.
Martin Gardner, Sixth Book of Mathematical Games pp 22-23 credits C. W.
Adams
John Hendricks. A magic Square Course, page 7, credits H.Lulli
The design is seen in many other books as well, with no credit given.
| Addendum: Sept. 12, 2002 Jerry Slocum mailed me a copy of an advertisement (?) dated 1896, crediting W. Radcliffe, Isle of Man, U.K. with this discovery in 1895. Jerry Slocum has a large collection of mechanical puzzles. See pictures here of two puzzles based on this magic hexagon as well as puzzles based on magic stars. (Click on this picture for an enlarged view). |
 |
![]()
An Order-9 pandiagonal Magic Square
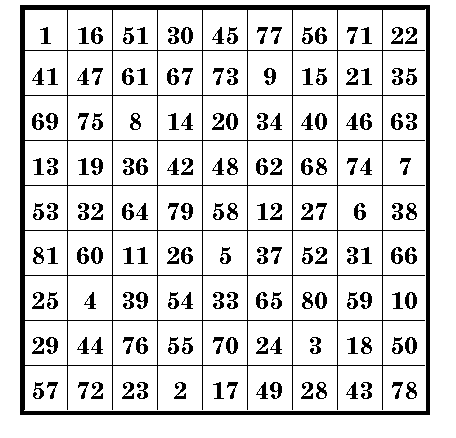
The general belief among magic square enthusiasts has been that it is impossible to construct a pandiagonal order-9 magic square.
However, in 1996 Mr. Gakuho Abe discovered a whole series of such squares.
See Dr. Alan Grogono's site at Magic Squares by "Grog" for more information.
This square is composed of the consecutive series of numbers from 1 to 81 and as is usual with pure magic squares, all rows, columns, and the two main diagonals sum to the constant 369.
Being pan-diagonal, the broken diagonals also sum to the magic constant. and the square can be transposed to another by moving any column or row to the opposite side.
![]()

![]() Please send me Feedback about my Web site!
Please send me Feedback about my Web site!
![]()
![]()
![]()
Harvey Heinz harveyheinz@shaw.ca
Last updated January 28, 2009
Copyright © 1998,2002 by Harvey D. Heinz