Polyominoes inside minimal circles

by Edo Timmermans

In 2002 Pieter Torbijn presented the article Polyominoes inside Circles in CFF 59, the magazine from the Dutch Cube Club. He gave permission to use the drawings from that article in this one. In CFF 61 and CFF63, I published tighter solutions for both pentominoes and heptominoes.

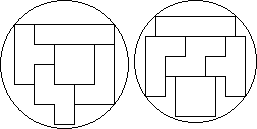
tetrominoes

In the drawing the tetrominoes are placed inside the (probably) smallest possible circles, without allowing shifting and including shifting. Pieter Torbijn found the solution on the left; the solution on the right is from Livio Zucca.

Note: Chris Anderson has pointed out that there is a smaller solution with a radius of 3.16 rather than Pieter Torbijn's 3.20.

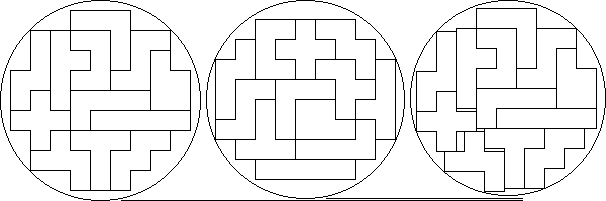
pentominoes

Pieter Torbijn found the solution in the middle, where the pentominoes are placed inside the smallest circle possible when shifting is not allowed. The radius is about 4.924.

The left solution is the basis for the solution on the right, before shifting. Before shifting the radius is 4.950, after shifting it is 4.876. The three most left pentominoes have been moved down 0.1560, the ones at the bottom have been moved 0.3823 to the right. Compared to the original position, the centre has moved 0.0756 to the right and 0.0289 upwards.

hexominoes

For hexominoes, the basis solution for shifting is also a best solution possible without shifting.

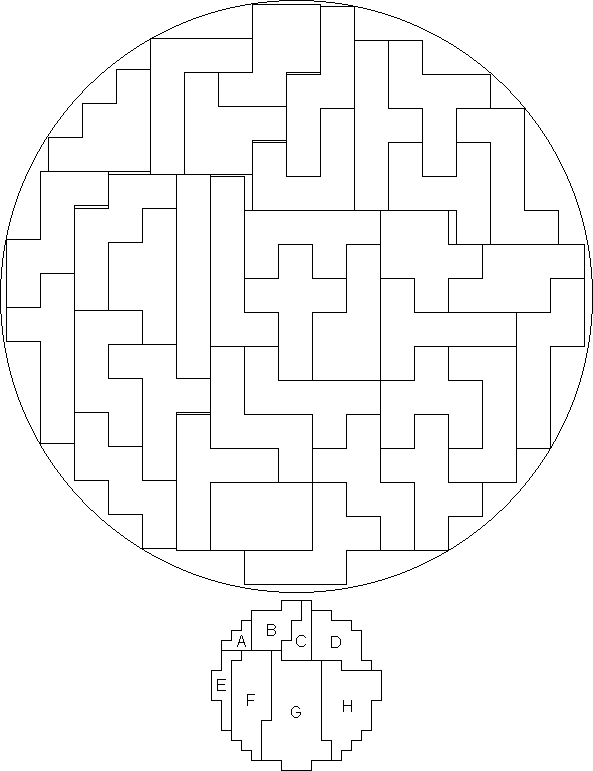
In the drawing above, parts A, B, C and D have been moved 0.25509244 to the right. Parts A, B, E and F have been moved 0.044796917 up, after which A and E were moved up another 0.076634982. The centre has moved 0.037068998 to the right and 0.030192144 down, compared to the original position. The solution fits in a circle with radius 8.7014816; the original radius was 8.746.

As the distance between part D and the circle is still 0.0000527, it is still possible to move D and H up a little bit. This makes it possible to squeeze the solution inside an even smaller circle. The improvement is so small, that it doesn't affect the drawing.

Heptominoes

The heptominoes fit inside a circle in such a perfect way, that most likely no solutions exist where shifting leads to placing the heptominoes inside a smaller circle. In 1988, Pieter Torbijn received the solution shown below from Maarten Bos.

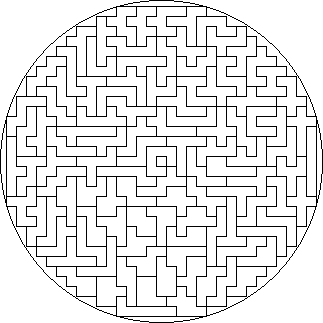
Heptomino Mandalas

Mandalas are works of art created by Buddhist monks that are usually both horizontally and vertically symmetrical, generally nicely fitting inside a circle. As the number of heptominoes (108) is a sacred number in both Buddhism and Hinduism, I decided to name the seven solutions below Heptomino Mandalas. I found them in July 2005.

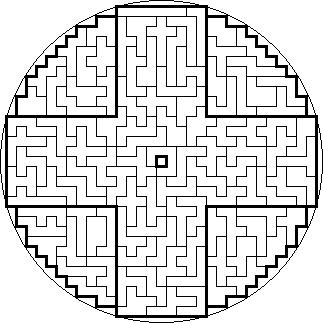
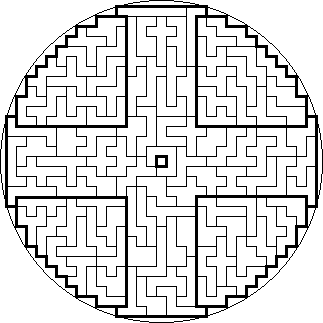
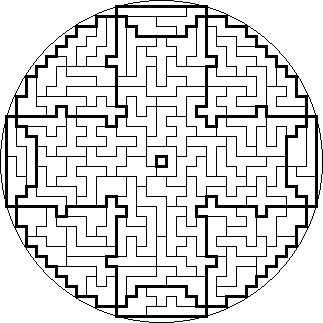
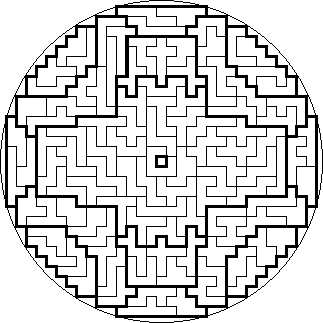
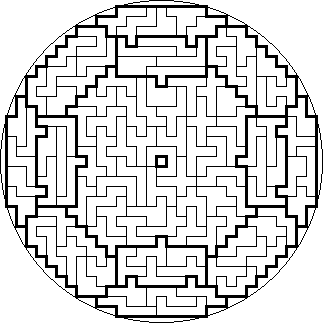
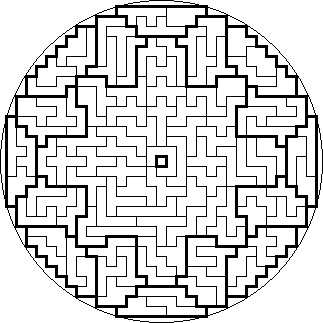
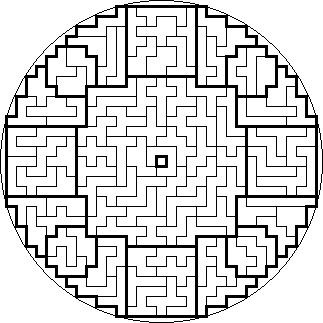
In the seventh Mandala there is so much symmetry present, that there are a record of 389,639,433,093,120 possible ways to place the 16 parts around the big central part. I think it will be very hard to break this record with a solution that is both horizontally and diagonally symmetrical, it might just be possible though.