![]()
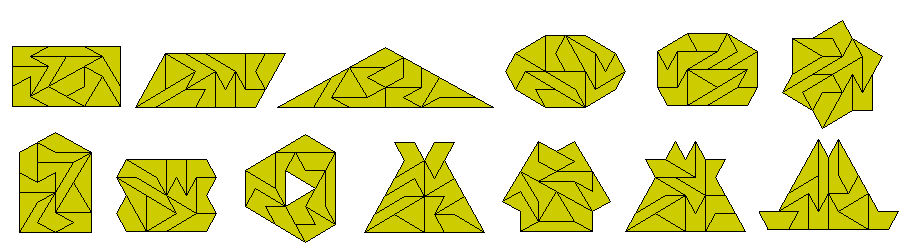
Jacques Ferroul has looked at the polyforms which can be produced from combining triangles and pons.The set with three of these consists of twelve pieces with an area of 36. Jacques has some of this information at his site. The set comprising three triangles and/or pons is shown below together with the colouring by triangles which shows that any figure must be balanced or a have a colour excess of 2, 4 or 6. Also shown are some figures made with the set.
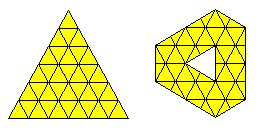
The triangle shown below is not possible as the pieces do not have sufficient edging to form the required border. The second shape here, although similar to one of the above may also be impossible.
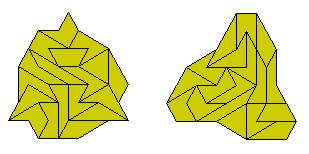
The one sided set consists of eighteen pieces with a total area of 54. This set is unbalanced in respect of colouring the triangles and so only rotationally symmetric constructions can be made.
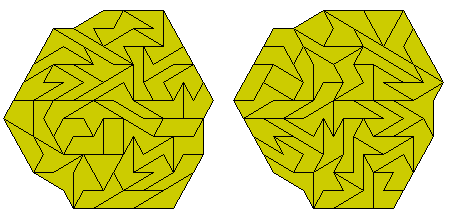
The one-sided set consists of 78 pieces and, being balanced, can form symmetrical figures.
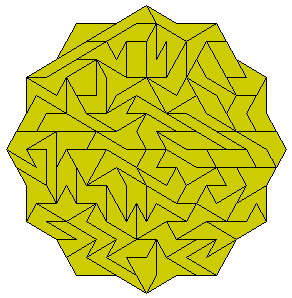
Peter Esser has made a rectangle with the set.

Sets of two and three congruent constructions are also possible.
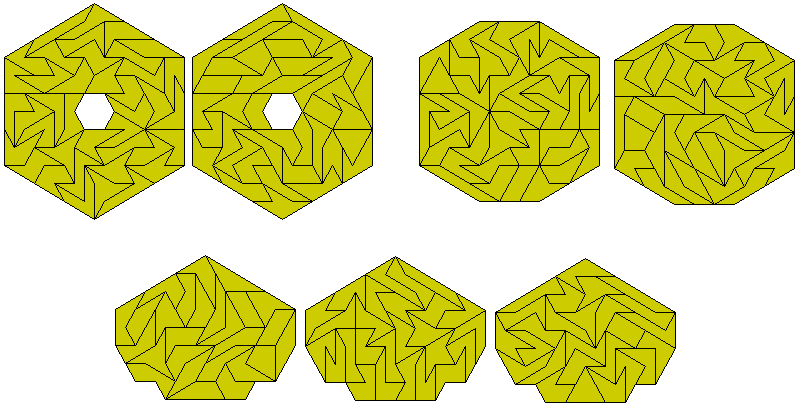
Six congruent constructions are also possible.Other examples below are by Peter Esser.
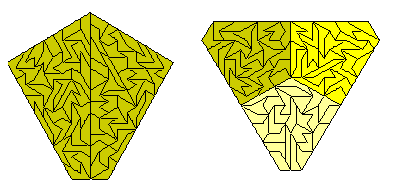

The 155 pieces without a hole can form five congruent figures.

This set can also form seven, nine or ten similar figures.
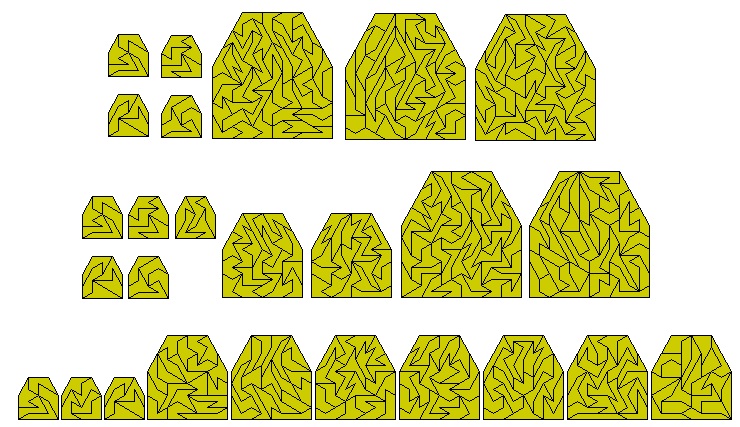

There are 295 one-sided pentiapons one of which has a hole. Omitting this piece Peter Esser has made a sevenfold replication of a pentahex.

Peter has made a number of other constructions with this set.
If we look at the chequered set of triiapons we get 21 pieces which can form a number of symmetrical figures.
