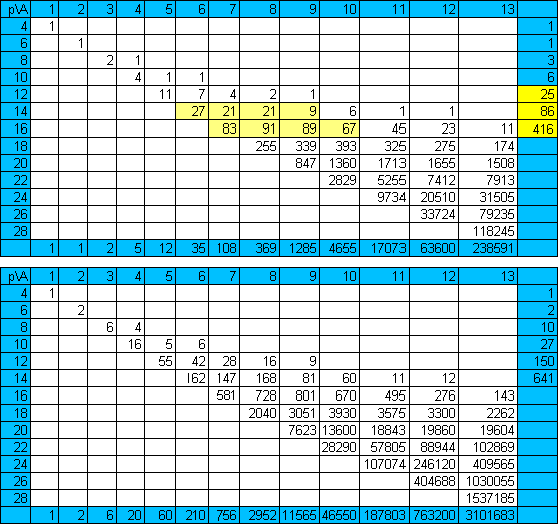
The following tables show (a) the numbers of polyominoes of a given area, A, and perimeter, P, and (b) the total areas of these sets of pieces. These tables were supplied by Brendan Owen. (Note: Livio Zucca has extended the idea of isoperimetry with his Polyedges.)
If we consider complete sets of a particular perimeter then we get the following -
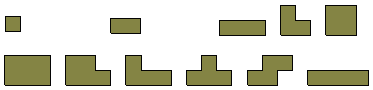
The polyominoes with perimeters 4, 6 , 8 and 10
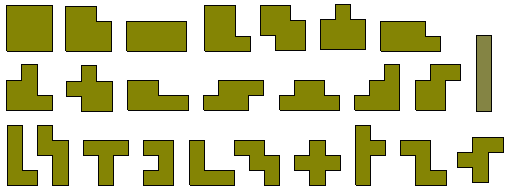
The 25 polyominoes with perimeter 12
The six polyominoes of perimeter 10 have a total area of 27 units and can be used to make a number of constructions three of which are shown below.The 25 polyominoes of perimeter 12 have a total area of 150 units.
Unlike the area fixed polyominoes we have no parity problems and there is a great variety of multiple constructions in which the areas of the parts are not fixed as a multiple of some fixed number.
Other constructions with the perimeter 12 set are shown here.
There are 36 one-sided polyominoes of perimeter 12 covering a total area of 213 unit squares. The only factorisation of 213 is 3x71 but this rectangle cannot be made owing to edging restrictions.
There are many ways of expressing 213 as the sum of squares giving the solutions below.
Fixed (translation only) Isoperimetric Polyominoes
Perimeter 10
Perimeter 12
712 can be decomposed into sums of squares in many ways ranging from the minimum of two squares up to the maximum known number of squares which can be made with the set. At present this is 25 as shown in the bottom figure below. This and the previous two solutions are by Patrick Hamlyn.
The maximum different squares which can be made is eight with ten possible sets.
The final figure shows a set of squares with two each of 4, 5, 7, 8, 9 and 11 as well as some square based constructions by Patrick Hamlyn.
If we allow 180° rotations of pieces we get what Peter Esser calls polarised sets of pieces. The 16 perimeter 10 pieces can form a 4x17 rectangle and the 70 perimeter 10 pieces while not forming any rectangle can make the series of squares shown below.