
Isoperimetrical Polyhexes
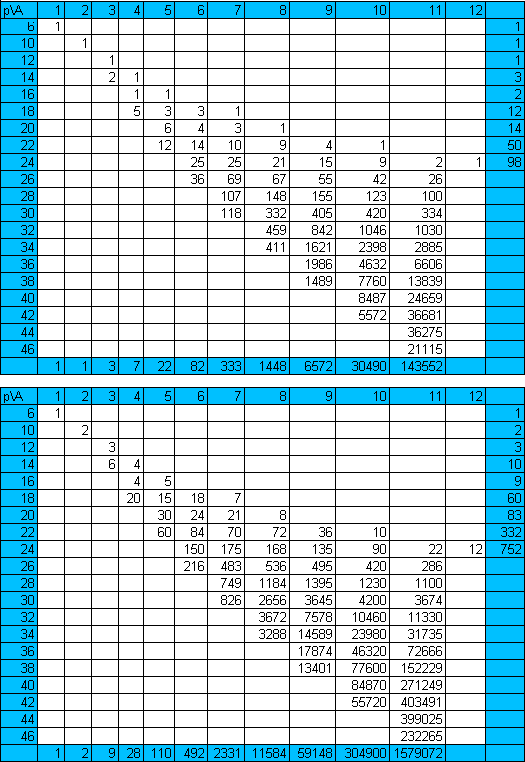
The following tables show (a) the numbers of polyominoes of a given area, A, and perimeter, P, and (b) the total areas of these sets of pieces. Brendan Owen has supplied these tables and the diagrams in the links (green areas).


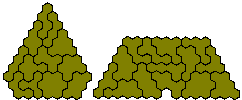
The diagram above shows the polyhexes with perimeters 6 to 16 and the following figures are made with the 12 pieces of perimeter 18 (left) and the 14 pieces of perimeter 20 (right).
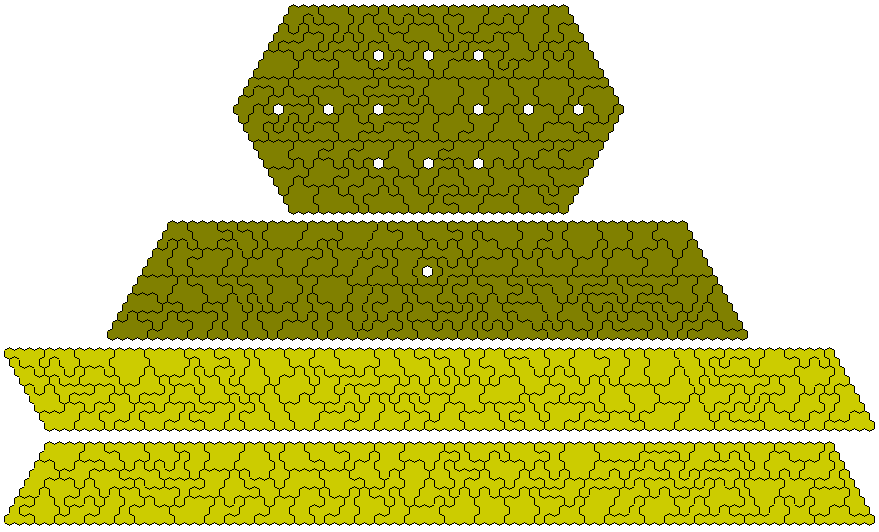
The perimeter 22 polyhexes cover a total area of 332 shown here forming a trapezium and sets of two and four congruent constructions.

The one-sided perimeter 22 set has 81 pieces with an area of 535. These can make a number of symmetric figures including a set of five congruent patterns.

The 98 perimeter 24 polyhexes include one piece with a hole. The remaining 97 pieces can for a 9x83 parallelogram and a 78-9 trapezium..