There are 82 hexahexes including one with a hole.

Other symmetrical constructions are also possible with this set.

Pairs of congruent shapes can also be made.

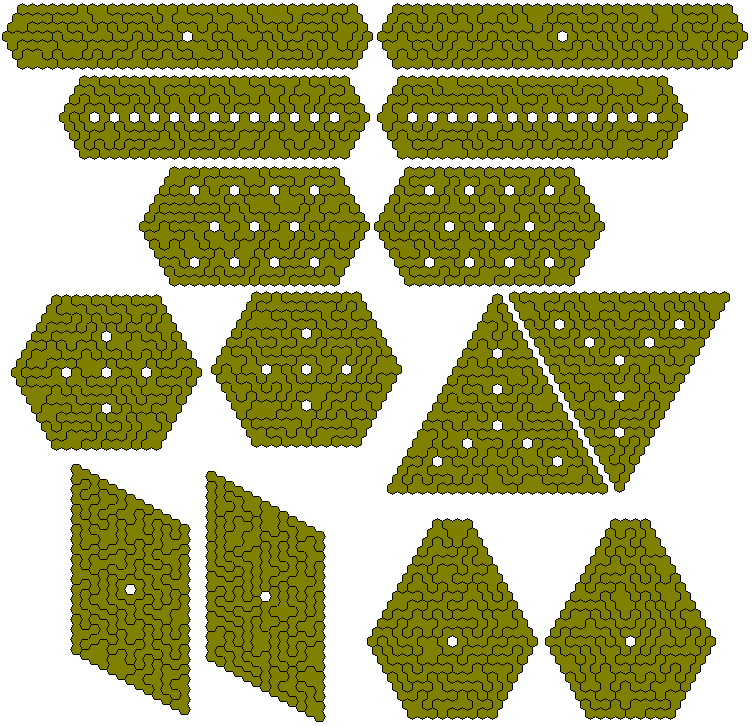
The construction below was made by Peter Esser.

The 81 pieces without a hole can form three 6x27, three 9x18 'parallelograms' and three trapezia.

A number of trapezia are also be possible - 50-9; 35-12; 5-27. The 120-4 which has the correct area is not possible since there are pieces which must divide the trapezium in two odd sized areas.

Nine congruent shapes can also be made with this set.

If we consider mirror pairs as distinct then there are 147 one-sided hexahexes shown in the construction below made by David Bird in 1973.

Other constructions with the set are shown below.

It is possible to make seven congruent shapes with this set.

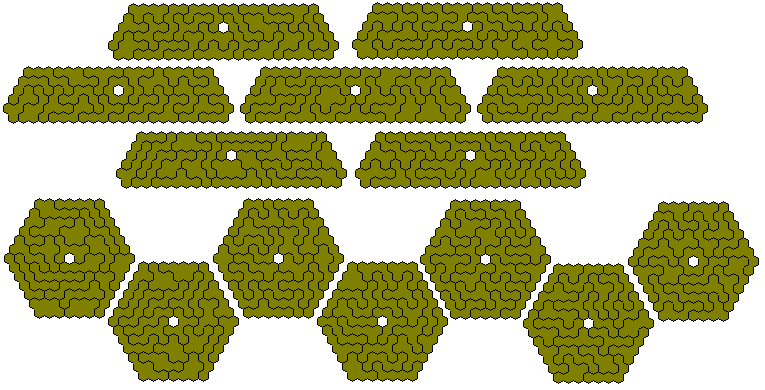
Peter Esser has made the strip below with this set.

The 146 pieces without a hole can form two 6x73 'parallelograms'.

The only possible trapezia for this set are the106-8 and the 25-24.