Polyabolos (PolyTans)
Die Polyabolos (auch als PolyTans bekannt) sind Formen, die durch verbundene Halbquadrate (diagonal geschnitten) entstehen. Es gibt ein Monabolo, drei Diabolos, vier Triaboloes and 14 Tetraboloes (siehe unten). Mehr Information über Tetrabolos ist bei Henri Picciotto's site, Michael Keller's Game and Puzzle Pages und Miroslav Vicher's polytans page zu finden. Auch Peter Esser hat bemerkenswerte Seiten mit Information über Polyabolos. Kadon Enterprises stellt Sätze von Polyabolos bis zu den Hexabolos her.
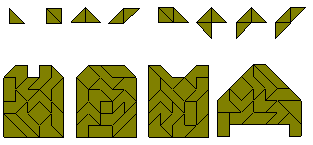
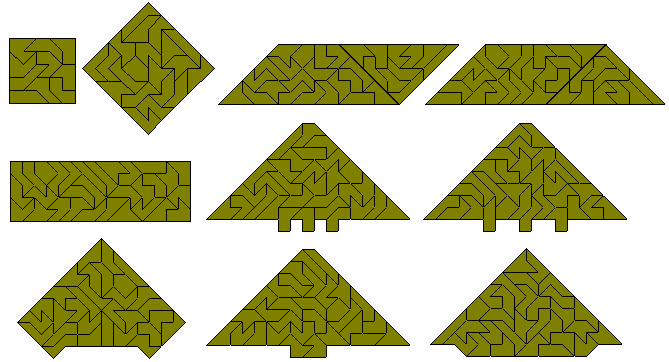
Es können Sätze von 2, 3, 5 oder 6 deckungsgleichen Formen gebildet werden. Man bemerke, dass aus den beiden Trapezen ein Parallelogramm, ein größeres Trapez and ein Rechteck gemacht werden kann. Drei 5x5 Qudrate hätten wohl die erforderliche Fläche, können aber nicht hergestellt werden, weil die Stücke nicht die erforderliche Anzahl Seitenteile enthalten. Es ist allerdings möglich, wie unten gezeigt, drei gleiche Dreiecke zu bilden.

Die Pentabolos können auch verwendet werden, um gleichzeitig ein- zwei- und fünffache Vervielfältigung eines Stücks zu bilden. Auch ein-, zwei-, drei- und vierfache Version ist möglich. Die größte Anzahl von Vervielfältigung ist sieben (einfach, viermal zweifach und dreifach), wie ganz unten im Bild gezeigt.
Ähnliche Konstruktionen können mit Vergrößerungsfaktoren gemacht werden, die ein Vielfaches von sind.

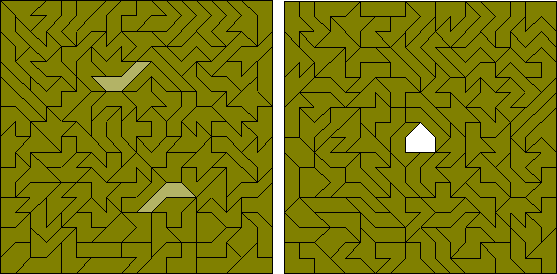
Es gibt 107 Hexabolos. Diese werden im Bild unten gezeigt, wo sie mit einer doppelt verwendeten Figur ein Quadrat bilden. Die Lösung links wurde um 1960 händisch gefunden. Die einzige weitere bekannte Lösung stammt von Anneke Treep aus 2001, wobei die zusätzliche Figur symmetrisch in der Mitte liegt.
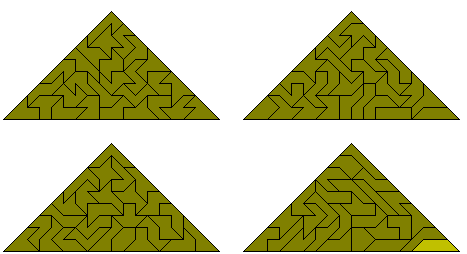
Peter Esser hat mit einer doppelten Figur vier deckungsgleiche Dreiecke gebildet
Obwohl aus den 107 Figuren kein Rechteck gebildet werden kann, ist es doch möglich, gleichzeitig ein-, fünf- und neunfache Vervielfältigungen herzustellen. Die Formen müssen eine ungerade Anzahl von diagonalen Seiten in beiden Richtungen haben, wie in dem Bild von Peter Esser unten zu sehen ist. Peter weist darauf hin, dass neben der Bedingung der ungeraden Seitenanzahl die 1-5-9-Vervielfältigung nur für ausgeglichene Figuren möglich ist, da es eine ungerade Anzahl von ausgeglichenen Figuren gibt, die zu einer ungeraden Anzahl von schwarzen Dreiecken führt, wenn man die ganze Konstruktion schachbrettartig färbt.

Da die Geamtfläche der Pentabolos 75 Quadrateinheiten beträgt, sollte eine Verfünffachung der Hexabolos mit dem Satz möglich sein. Fünf Beispiele sind unten gezeigt. Auf Peter Esser's site sind für alle 107 Fälle Lösungen zu finden.
Einseitige Polyabolos
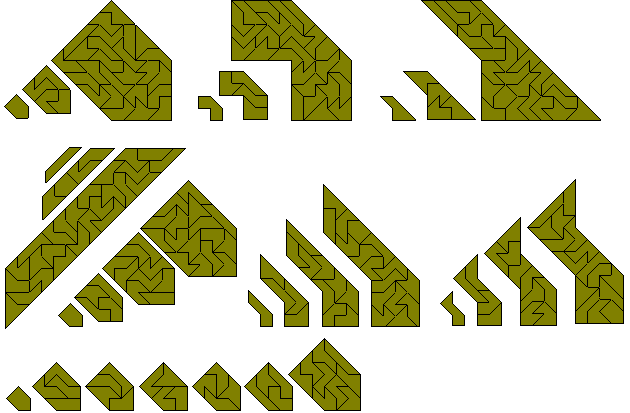
Die Konstruktionen unten bestehen aus den 22 einseitigen Tetrabolos
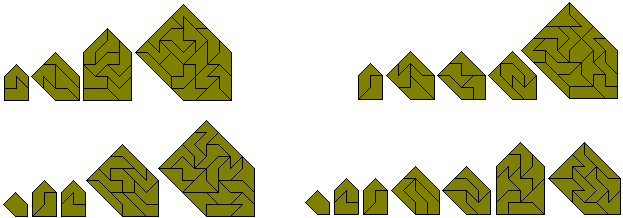
Es gibt 56 einseitige Pentabolos, die im Bild unten verwendet werden, um mit den Figuren verschiedene Serien von ähnlichen Formen zu bilden. Mehr Formen mit einseitigen Pentabolos sind in Peter Esser's constructions with the one-sided pentaboloes zu finden.
Das nächste Bild zeigt einige Serien von deckungsgleichen Formen mit dem Satz.
letzte Bild sind Beispiele von Lösungen mit einem Loch ähnlich der äußeren Form. Peter Esser hat auch für diese Art Konstruktionen mit einseitigen Pentabolos eine Sammlung auf Peter's site.