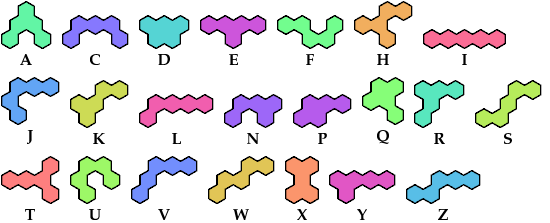
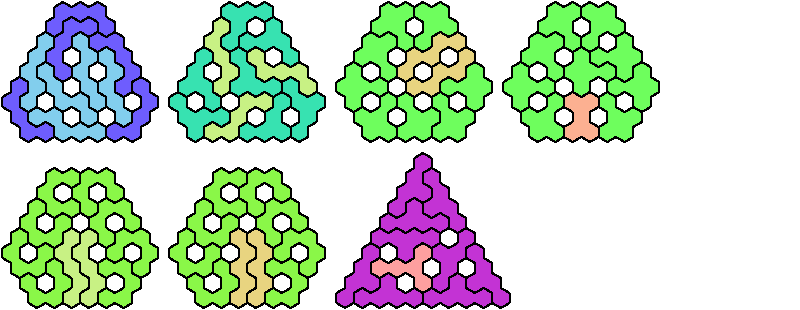
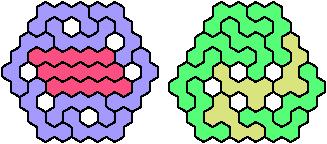
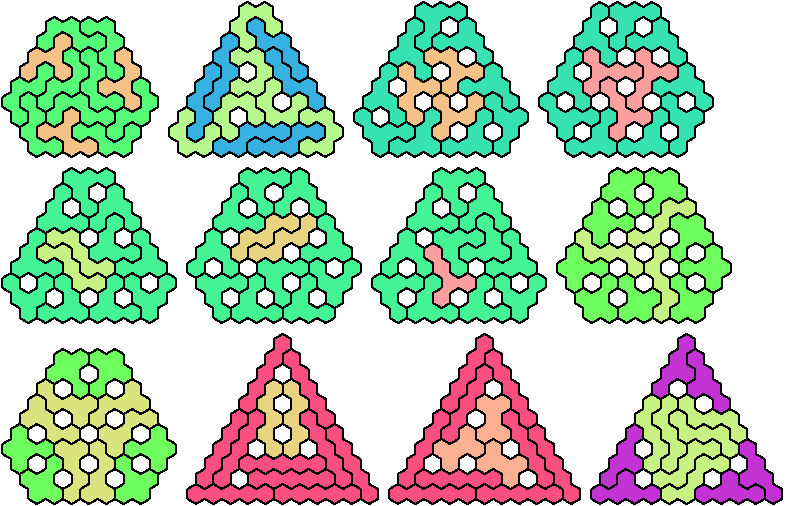
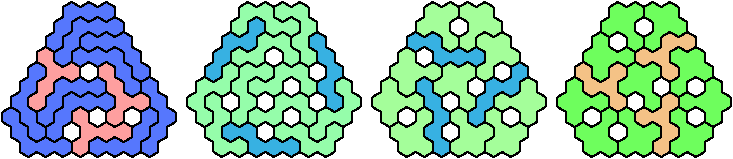
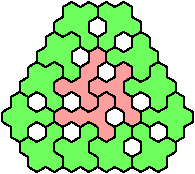
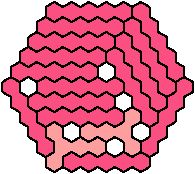
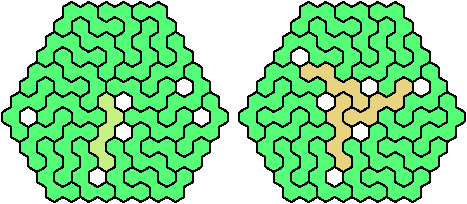
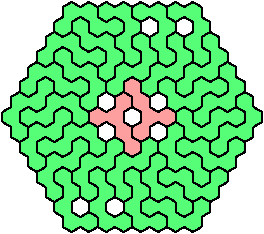
Let a polyhex badge be a polyhex whose cell centers form a convex hexagon whose alternate sides have equal length. Here I study the problem of arranging copies of two given pentahexes to form a badge, allowing 1-cell holes in the badge.
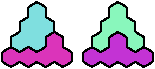
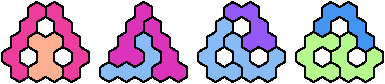
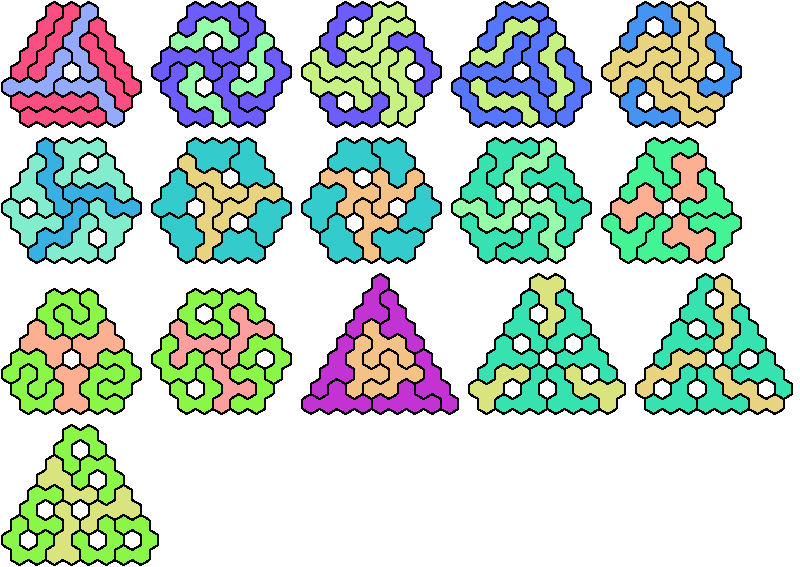
A triangular polyhex is an extreme form of a badge. Many of the solutions below are triangular. See the bottom of the page for non-triangular variants.

| A | C | D | E | F | H | I | J | K | L | N | P | Q | R | S | T | U | V | W | X | Y | Z | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | • | 8 | 4 | 2 | 6 | 8 | 4 | 6 | 7 | 5 | 4 | 5 | 6 | 7 | 12 | 12 | 6 | 5 | 12 | 9 | 4 | 8 |
| C | 8 | • | 5 | 6 | 9 | 7 | 11 | 6 | 8 | 6 | 5 | 5 | 5 | 6 | 9 | 6 | 6 | 7 | 5 | 5 | 6 | 10 |
| D | 4 | 5 | • | 5 | 6 | 9 | 4 | 6 | 6 | 5 | 5 | 5 | 5 | 5 | 7 | 8 | 6 | 5 | 9 | 6 | 2 | 8 |
| E | 2 | 6 | 5 | • | 6 | 9 | 4 | 6 | 6 | 7 | 5 | 4 | 6 | 8 | 12 | 10 | 5 | 6 | 6 | 6 | 6 | 7 |
| F | 6 | 9 | 6 | 6 | • | 12 | 6 | 8 | 11 | 6 | 7 | 5 | 7 | 9 | 24 | 32 | 6 | 8 | 24 | 7 | 4 | 13 |
| H | 8 | 7 | 9 | 9 | 12 | • | 6 | 6 | — | 6 | 5 | 6 | 13 | 12 | — | — | 6 | 6 | — | — | 8 | — |
| I | 4 | 11 | 4 | 4 | 6 | 6 | • | 6 | 6 | 6 | 5 | 5 | 6 | 8 | 6 | 17 | 7 | 9 | 12 | 12 | 4 | 7 |
| J | 6 | 6 | 6 | 6 | 8 | 6 | 6 | • | 5 | 5 | 3 | 5 | 6 | 5 | 5 | 6 | 3 | 5 | 9 | 5 | 3 | 6 |
| K | 7 | 8 | 6 | 6 | 11 | — | 6 | 5 | • | 5 | 5 | 5 | 12 | 9 | — | — | 9 | 5 | — | — | 4 | — |
| L | 5 | 6 | 5 | 7 | 6 | 6 | 6 | 5 | 5 | • | 5 | 5 | 5 | 6 | 7 | 6 | 5 | 7 | 6 | 3 | 6 | 6 |
| N | 4 | 5 | 5 | 5 | 7 | 5 | 5 | 3 | 5 | 5 | • | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 8 | 5 | 4 | 6 |
| P | 5 | 5 | 5 | 4 | 5 | 6 | 5 | 5 | 5 | 5 | 5 | • | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 4 | 5 |
| Q | 6 | 5 | 5 | 6 | 7 | 13 | 6 | 6 | 12 | 5 | 5 | 5 | • | 6 | 12 | 15 | 6 | 5 | 10 | 10 | 7 | 13 |
| R | 7 | 6 | 5 | 8 | 9 | 12 | 8 | 5 | 9 | 6 | 5 | 5 | 6 | • | 10 | 12 | 5 | 7 | 9 | 7 | 6 | 9 |
| S | 12 | 9 | 7 | 12 | 24 | — | 6 | 5 | — | 7 | 5 | 5 | 12 | 10 | • | — | 10 | 9 | — | — | 7 | — |
| T | 12 | 6 | 8 | 10 | 32 | — | 17 | 6 | — | 6 | 5 | 5 | 15 | 12 | — | • | 9 | 13 | — | — | 8 | — |
| U | 6 | 6 | 6 | 5 | 6 | 6 | 7 | 3 | 9 | 5 | 5 | 5 | 6 | 5 | 10 | 9 | • | 6 | 10 | 9 | 6 | 12 |
| V | 5 | 7 | 5 | 6 | 8 | 6 | 9 | 5 | 5 | 7 | 5 | 5 | 5 | 7 | 9 | 13 | 6 | • | 5 | 7 | 7 | 7 |
| W | 12 | 5 | 9 | 6 | 24 | — | 12 | 9 | — | 6 | 8 | 5 | 10 | 9 | — | — | 10 | 5 | • | — | 6 | — |
| X | 9 | 5 | 6 | 6 | 7 | — | 12 | 5 | — | 3 | 5 | 5 | 10 | 7 | — | — | 9 | 7 | — | • | 6 | — |
| Y | 4 | 6 | 2 | 6 | 4 | 8 | 4 | 3 | 4 | 6 | 4 | 4 | 7 | 6 | 7 | 8 | 6 | 7 | 6 | 6 | • | 4 |
| Z | 8 | 10 | 8 | 7 | 13 | — | 7 | 6 | — | 6 | 6 | 5 | 13 | 9 | — | — | 12 | 7 | — | — | 4 | • |






Last revised 2026-01-02.