
The compatibility problem
is to find a figure that can be tiled with each of a set of polyforms.
Polyomino compatibility has been widely studied since 1992, when
Pablo Coll first posed and studied the problem for pentominoes.
Two well-known websites, Poly2ominoes by Jorge Mireles and
Polypolyominoes by
Giovanni Resta, present the results of their authors' systematic searches
for compatibility figures.
Mireles's site includes solutions by other researchers, especially Mike Reid.
So far as I know, polyomino compatibility has not been treated in print
since Golomb first raised the issue in 1981,
except in Issue 3 of Rodolfo Marcelo Kurchan's
periodical Puzzle Fun (1995), and
in a series of articles called Polyomino Number Theory,
written by Andris Cibulis, Andy Liu, Bob Wainwright,
Uldis Barbans, and Gilbert Lee from 2002 to 2005.
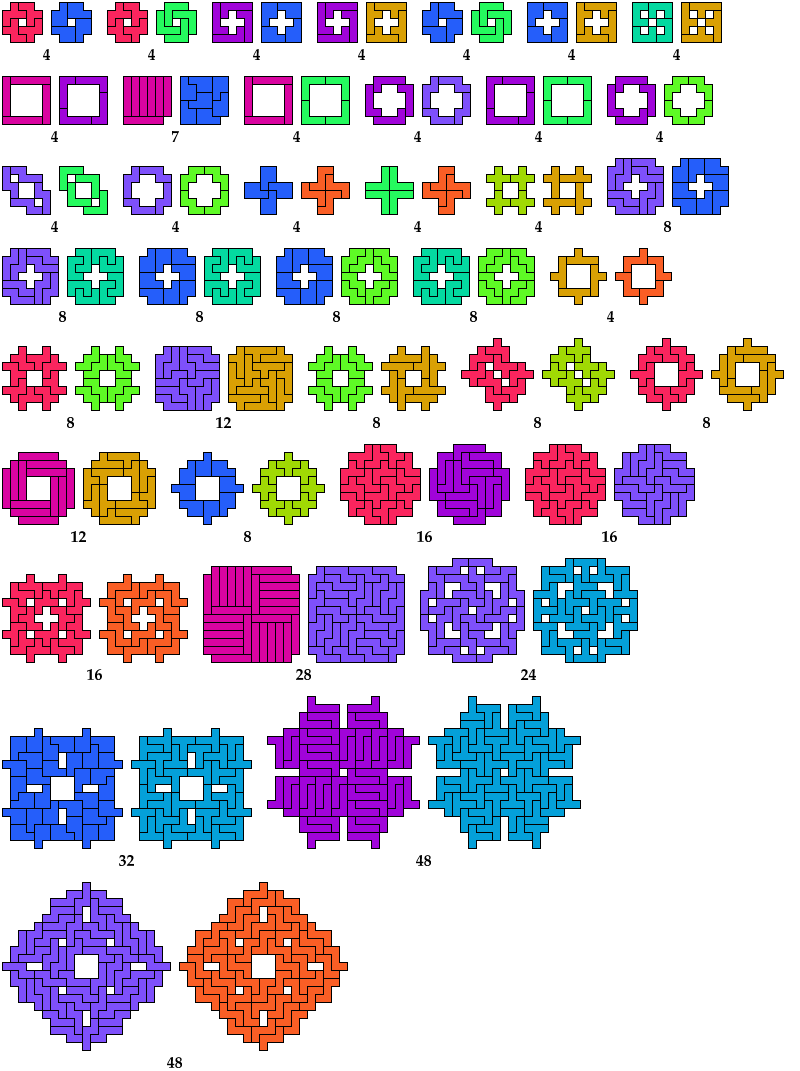
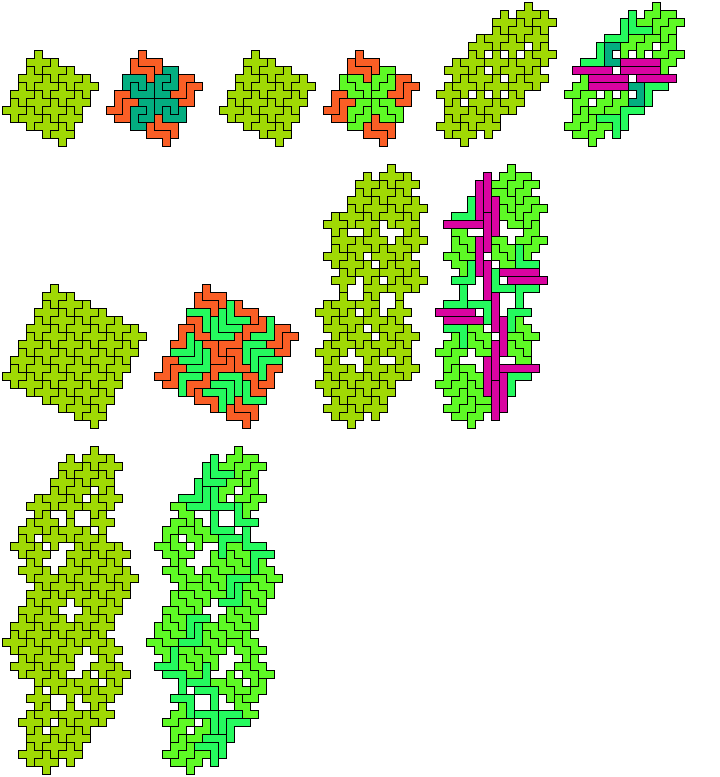
The websites and the articles present a wealth of polyomino compatibilities. They do not show all current results. I do so below, for pentomino-pentomino compatibility only. I am not prepared to maintain a current catalogue of results for other kinds of pairs of polyominoes, or for larger sets such as the pentomino triples that Livio Zucca has collected here.
I also show holeless variants. So far as I know, these have been covered before only in Puzzle Fun.
For compatibility figures with an odd number of tiles, see Livio Zucca's Pentomino Odd Pairs. For Galvagni compatibility (self-compatibility), see Galvagni Figures & Reid Figures for Pentominoes.

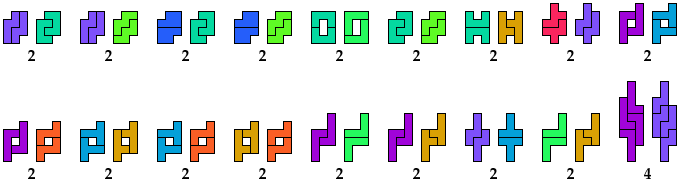
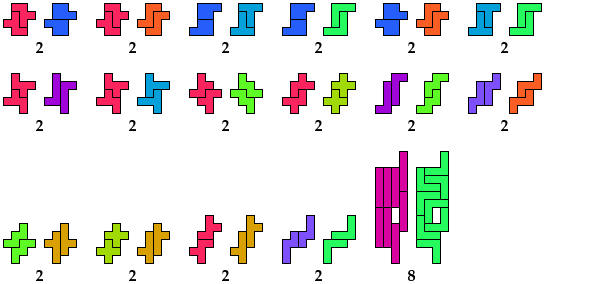
| F | I | L | N | P | T | U | V | W | X | Y | Z | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F | * | 10 | 2 | 2 | 2 | 2 | 4 | 4 | 2 | 2 | 2 | 2 |
| I | 10 | * | 2 | 2 | 2 | 4 | 12 | 4 | 10 | × | 2 | 20 |
| L | 2 | 2 | * | 4 | 2 | 2 | 2 | 2 | 2 | 44 | 2 | 2 |
| N | 2 | 2 | 4 | * | 2 | 2 | 2 | 2 | 2 | 16 | 2 | 2 |
| P | 2 | 2 | 2 | 2 | * | 2 | 2 | 2 | 2 | 4 | 2 | 2 |
| T | 2 | 4 | 2 | 2 | 2 | * | 4 | 2 | 14 | 4 | 2 | 2 |
| U | 4 | 12 | 2 | 2 | 2 | 4 | * | 2 | 2 | × | 2 | 4 |
| V | 4 | 4 | 2 | 2 | 2 | 2 | 2 | * | 6 | × | 2 | 4 |
| W | 2 | 10 | 2 | 2 | 2 | 14 | 2 | 6 | * | ? | 2 | 4 |
| X | 2 | × | 44 | 16 | 4 | 4 | × | × | ? | * | 2 | ? |
| Y | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | * | 2 |
| Z | 2 | 20 | 2 | 2 | 2 | 2 | 4 | 4 | 4 | ? | 2 | * |
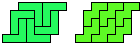

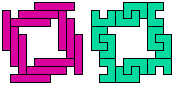
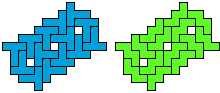
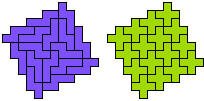
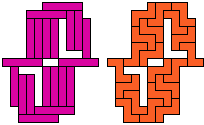
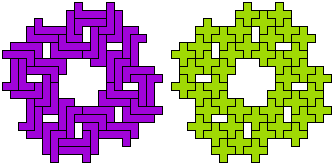


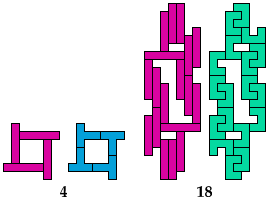
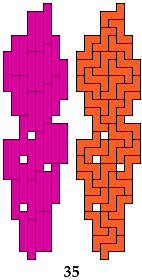
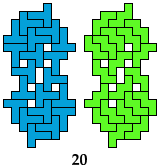
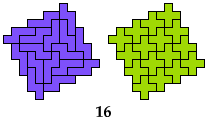
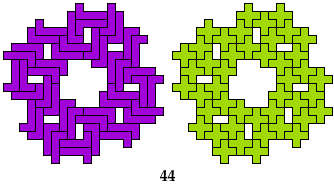
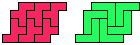
Are there any other hybrid solutions?

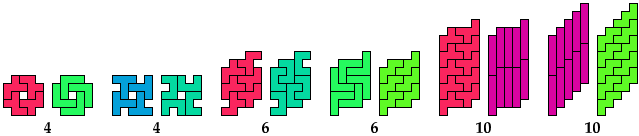
| F | I | L | N | P | T | U | V | W | X | Y | Z | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F | * | 10 | 2 | 2 | 2 | 2 | 4 | 6 | 2 | 2 | 2 | 2 |
| I | 10 | * | 2 | 2 | 2 | 32 | ? | 10 | 10 | × | 2 | ? |
| L | 2 | 2 | * | 4 | 2 | 2 | 2 | 2 | 2 | × | 2 | 2 |
| N | 2 | 2 | 4 | * | 2 | 2 | 2 | 2 | 2 | 16 | 2 | 2 |
| P | 2 | 2 | 2 | 2 | * | 2 | 2 | 2 | 2 | 4 | 2 | 2 |
| T | 2 | 32 | 2 | 2 | 2 | * | ? | 2 | 16 | 4 | 2 | 30 |
| U | 4 | ? | 2 | 2 | 2 | ? | * | ? | 2 | × | 2 | ? |
| V | 6 | 10 | 2 | 2 | 2 | 2 | ? | * | 6 | × | 2 | 4 |
| W | 2 | 10 | 2 | 2 | 2 | 16 | 2 | 6 | * | ? | 2 | 10 |
| X | 2 | × | × | 16 | 4 | 4 | × | × | ? | * | 2 | ? |
| Y | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | * | 2 |
| Z | 2 | ? | 2 | 2 | 2 | 30 | ? | 4 | 10 | ? | 2 | * |
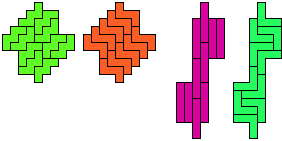
Last revised 2022-04-17.