Tiling a Triangle with a Scaled Polyiamond

Introduction

When can a polyiamond at various scales tile a triangle? Here I show some minimal known tilings of triangles by scaled copies of a polyiamond. Please write if you know of other such tilings.

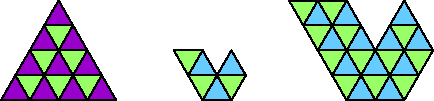
Tilings found by Carl Schwenke and Johann Schwenke are marked with §.

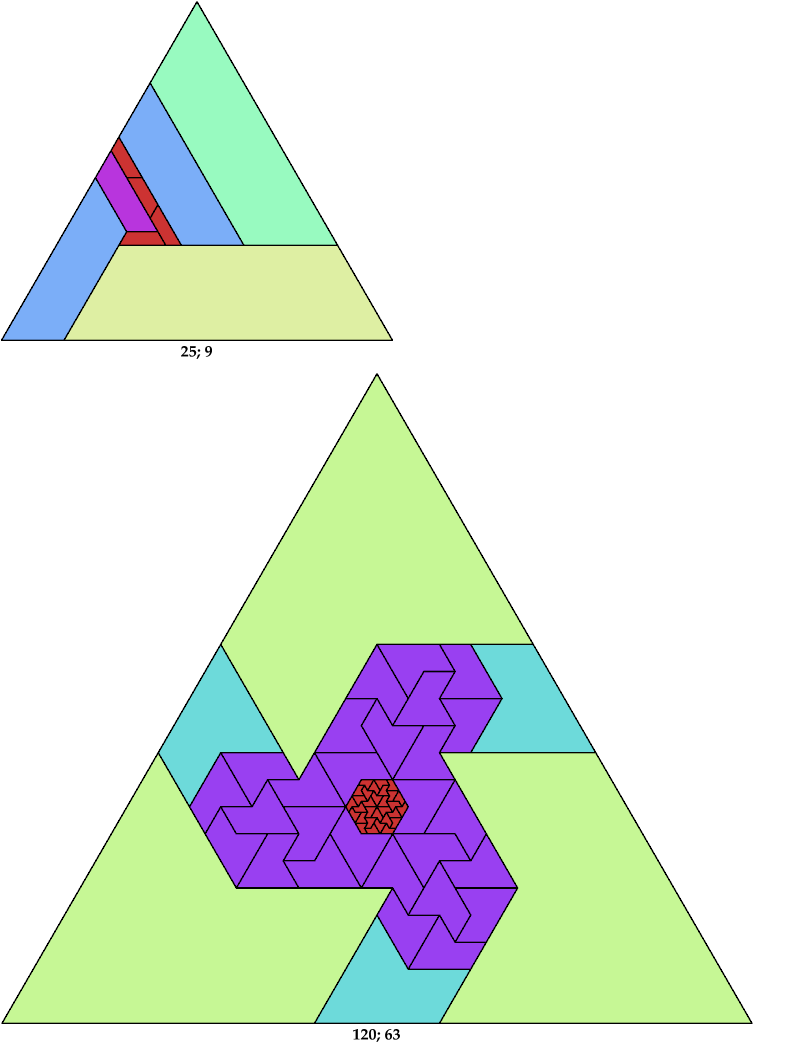
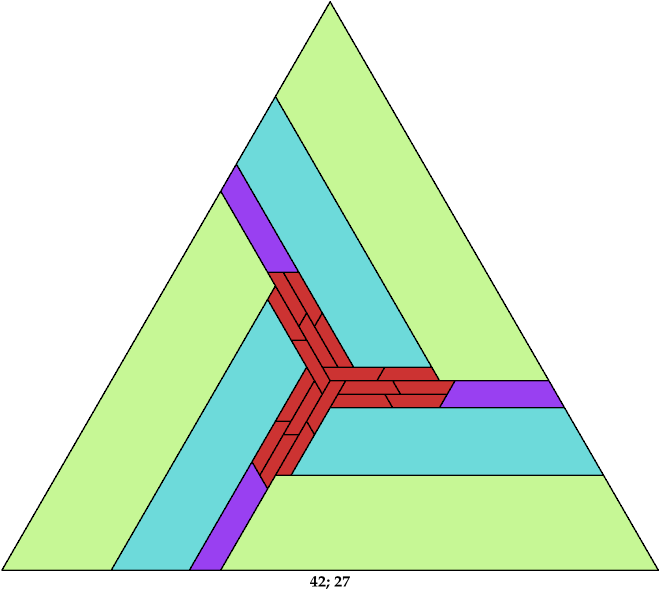
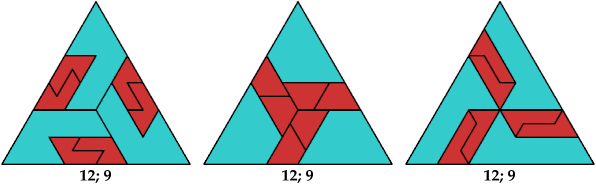
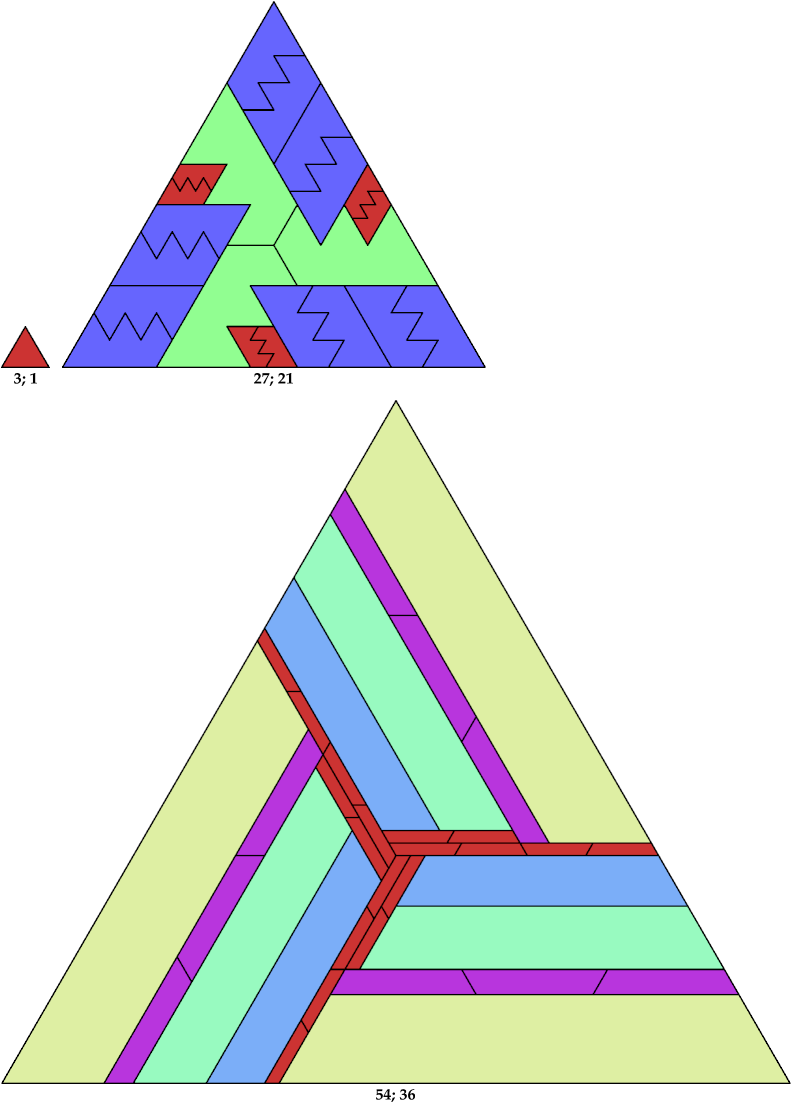
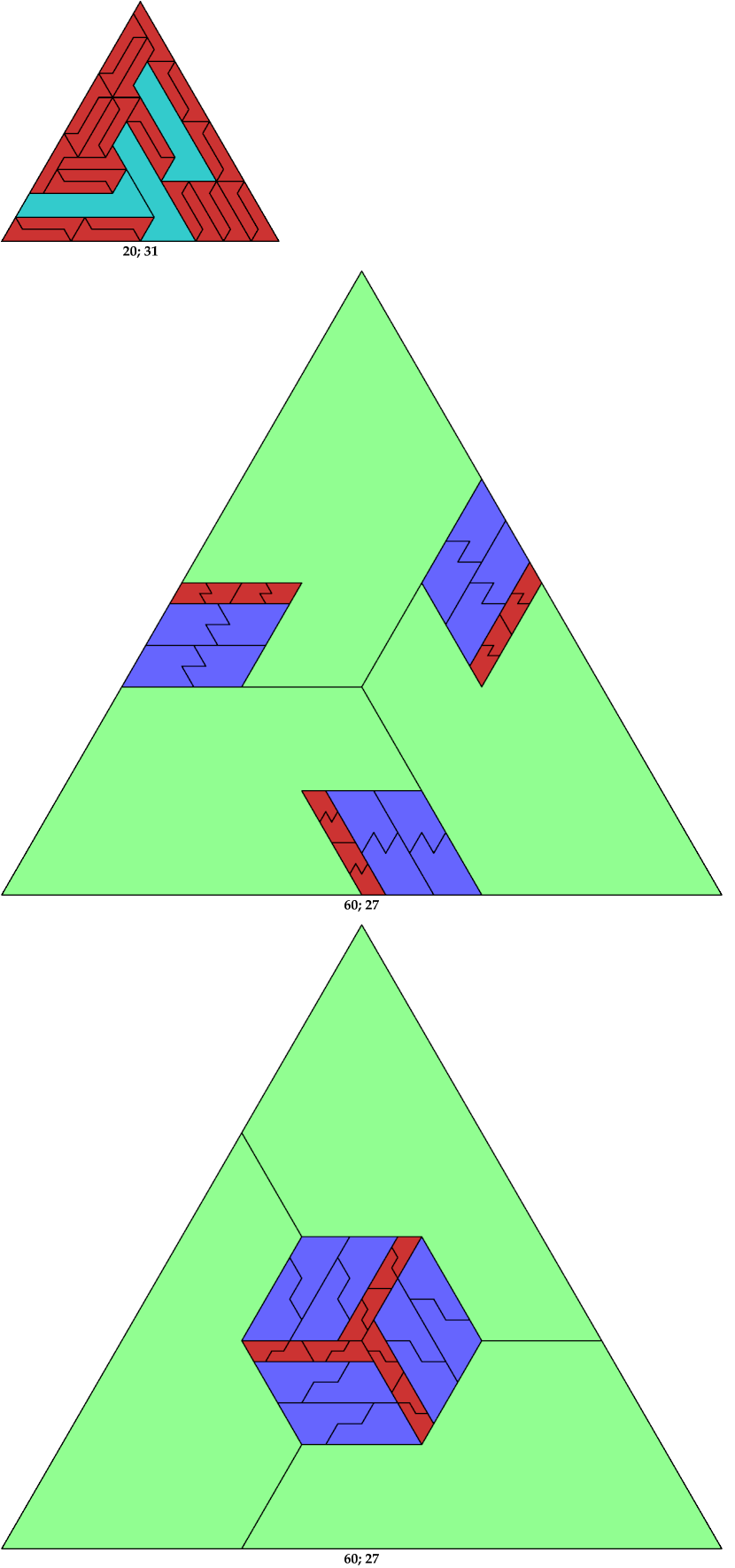
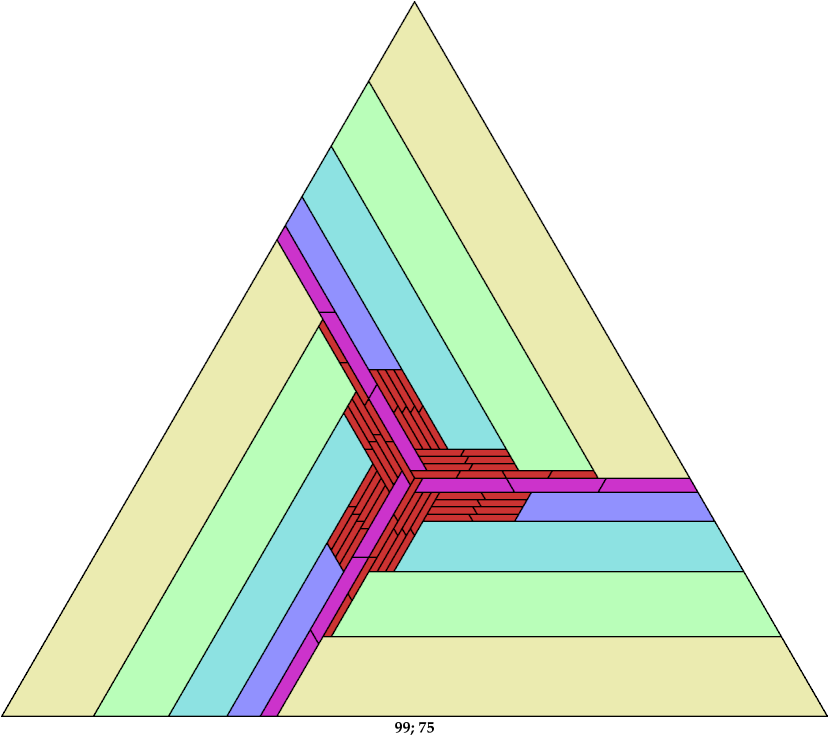
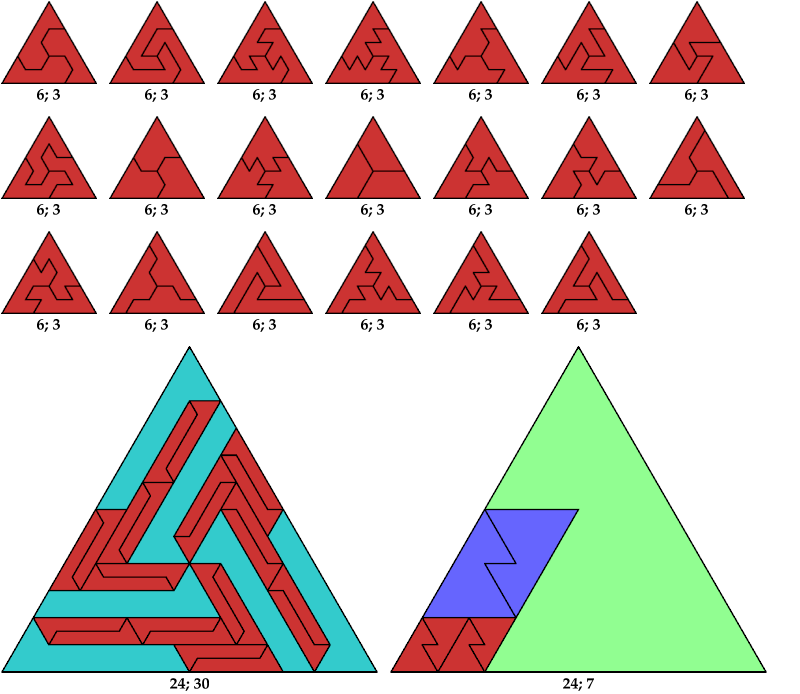
Here I show the solution with the fewest known tiles for each polyiamond. In the figures below, the numbers are the side of the triangle and the number of tiles used.

General Results

Cell Parity

Every triangular polyiamond has an imbalance of cells pointing up and cells pointing down. Thus any polyiamond whose cell parity balances cannot tile a triangle. Even when scaled up, such a polyiamond has equal numbers of cells pointing up and cells pointing down.

Straight Polyiamonds

With scaling, every straight polyiamond with an odd number of cells can tile a triangle. The method is shown below, applied to the straight heptiamond.

Scaled copies of the straight heptiamond may be stacked to form a bigger trapezium (trapezoid, in Canada and the U.S.):

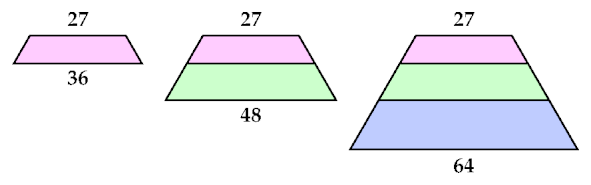
Stack the tiles thus till the longer base of the trapezium is at least twice as long as the shorter base. In the stack on the right, the longer base has length 64 and the shorter base has length 27. This satisfies the condition.

Now join a parallelogram to one end of the trapezium so that the short base becomes equal to the slant height:

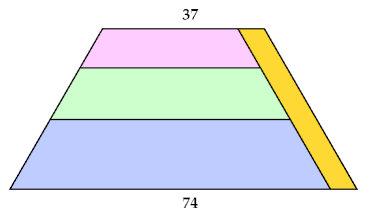
The parallelogram in the diagram has dimensions 10 × 37. Two straight heptiamonds can form a parallelogram with dimensions 2 × 7. If we scale up the tiling shown above, such 2 × 7 parallelograms can tile the yellow parallelogram.

The padded tiling forms a triamond. Arrange three copies of this triamond tiling to form a triangle:

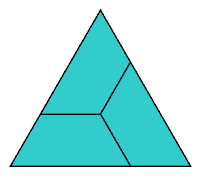
This method applies to any trapezial polyiamond, whether or not its slant height is 1.

Mike Reid stated that any straight polyiamond with an odd number of cells can tile a triangle, even without being scaled. He is not known to have published a proof.