Scaled Polytan Tetrads

Introduction

In plane geometry, a tetrad is an arrangement of four congruent shapes in which each borders the other three. See Polyform Tetrads.

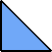
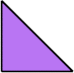
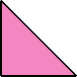
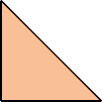
At his website Atlantis, Dr. Karl Scherer introduced similar or scaled tetrads. These are arrangements of four similar shapes in which each borders the other three.

In general, scaled tetrads are easier to find that standard tetrads. Scherer's page showed how the right tromino can form scaled tetrads. The smallest polyominoes that can form standard tetrads have eight cells.

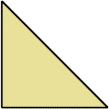
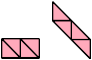
Scherer proved that convex shapes cannot form tetrads. However, some can form scaled tetrads, as shown below.

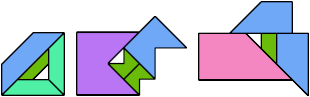
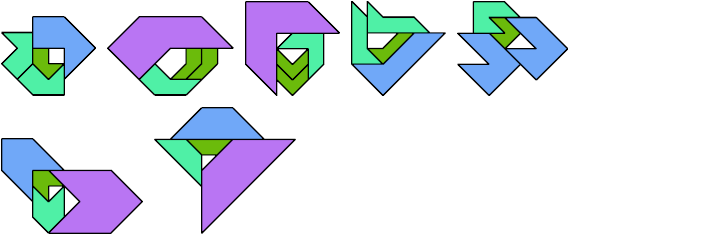
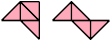
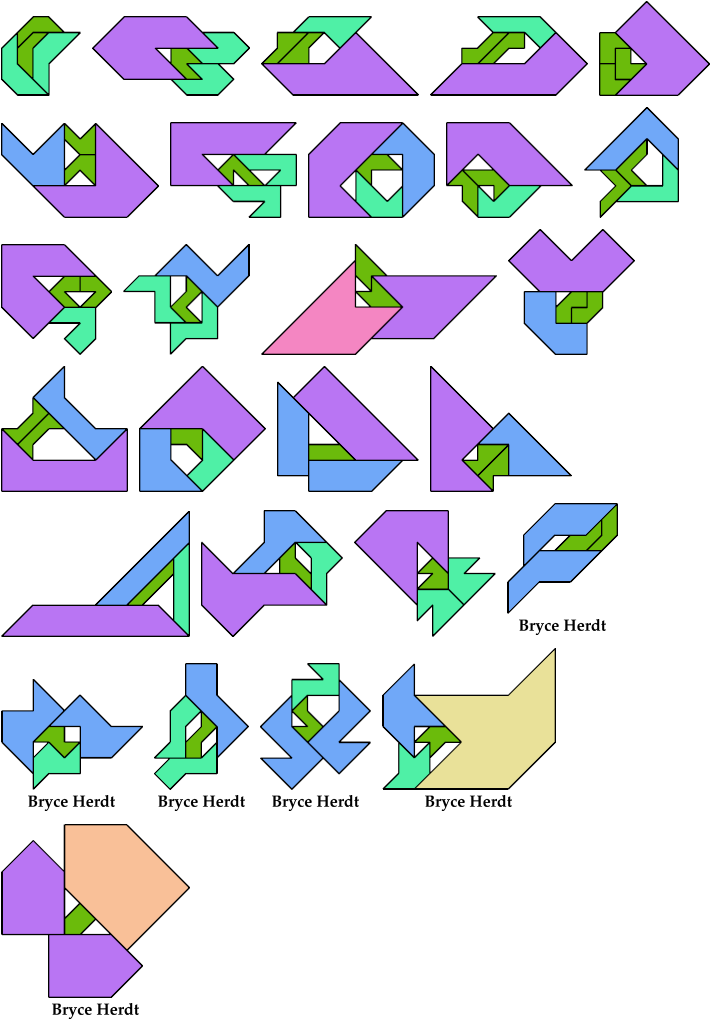
Here I show the smallest known scaled tetrads for polytans with 3, 4, or 5 cells, using scale factors that are integers or integer multiples of √2. If you find a smaller solution or solve an unsolved case, please write.

Bryce Herdt found smaller solutions for some pentatans.