Tiling Isosceles Trapezia with Scaled Pentabolo Pairs

Introduction

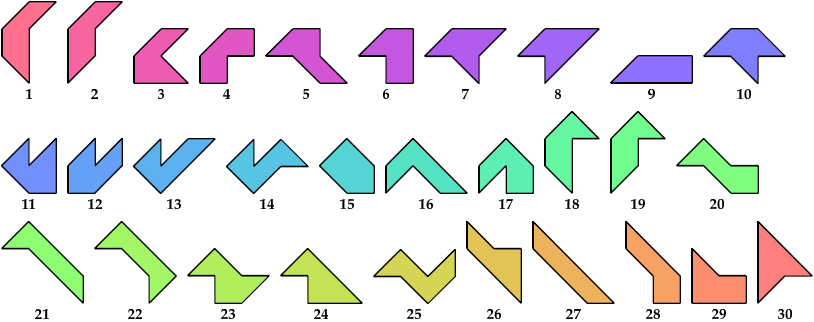
A scaled pentabolo is a pentabolo whose size may be altered without changing its shape. In geometric terms, it is a family of similar pentaboloes.

A trapezium (trapezoid in Canada and the U.S.) is a plane figure with four sides, two of them parallel. A isosceles trapezium is a trapezium whose two non-parallel sides have the same length.

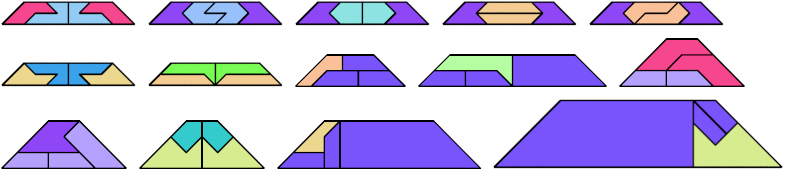
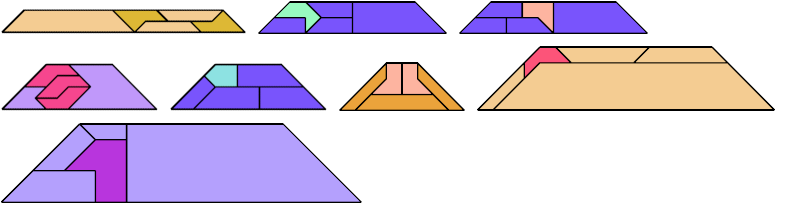
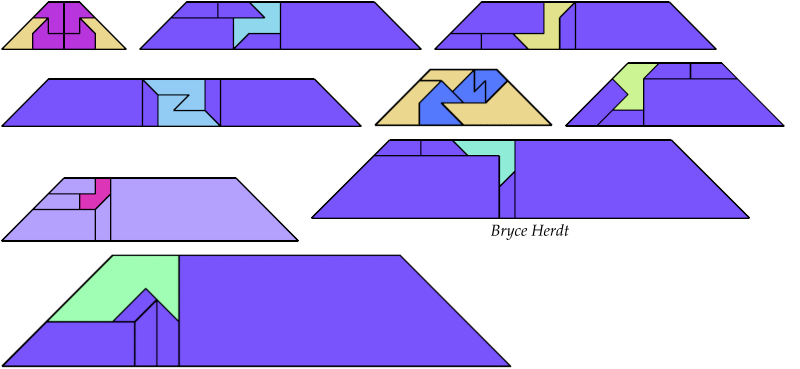
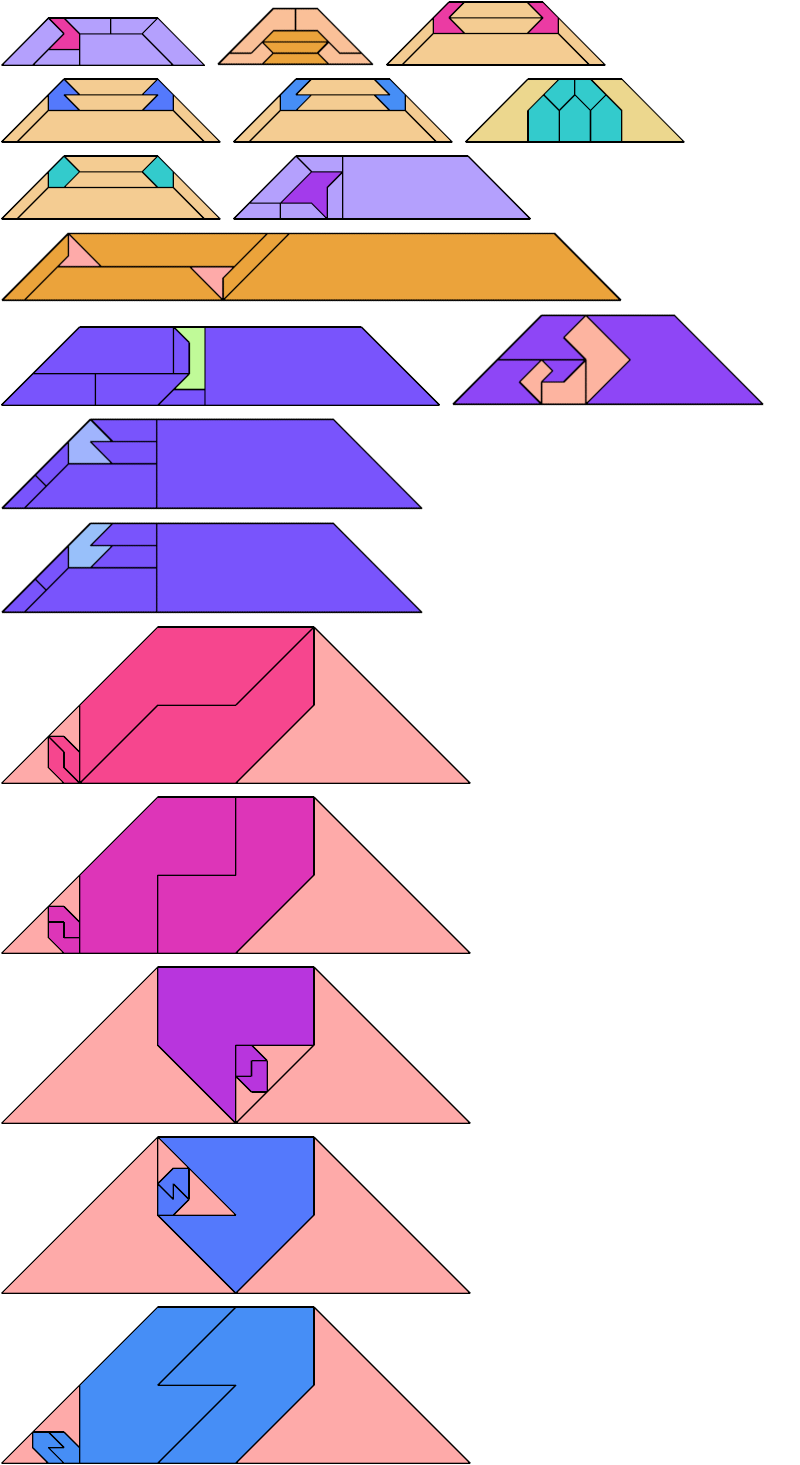
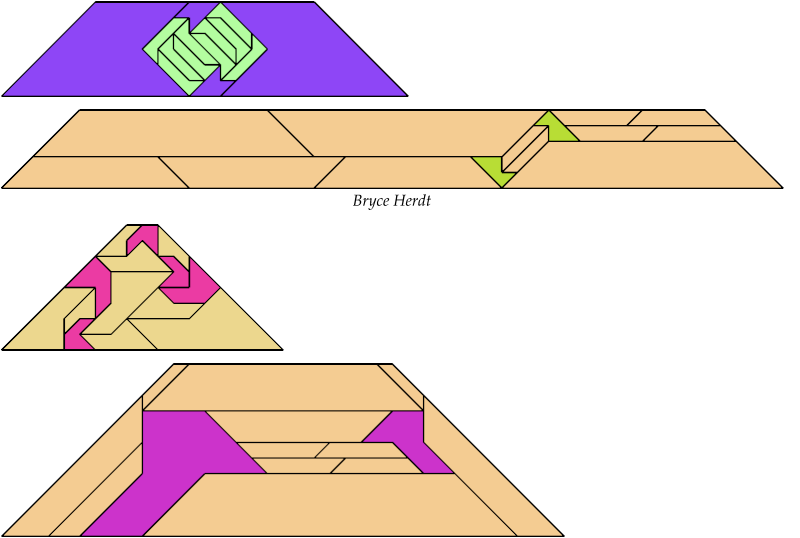
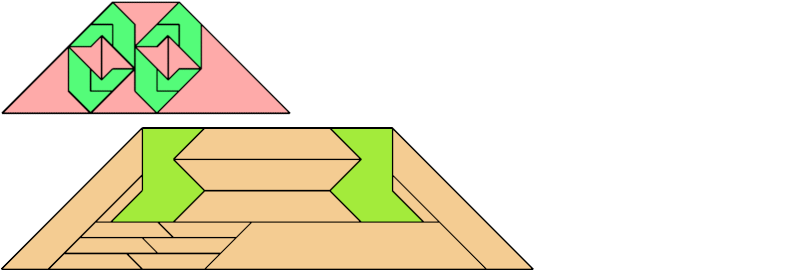
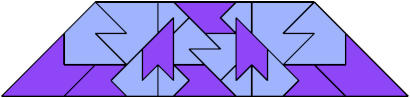
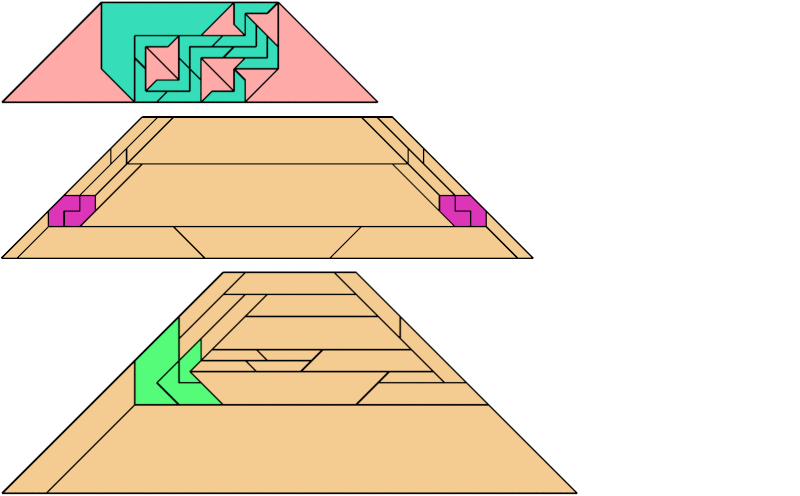
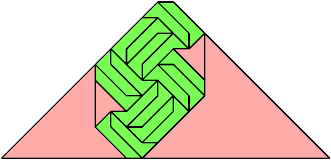
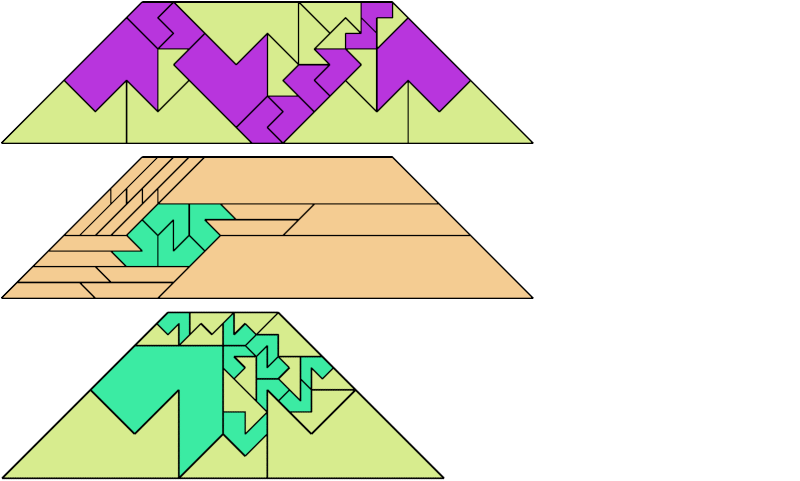
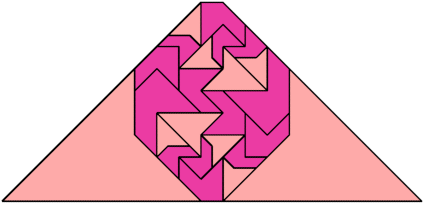
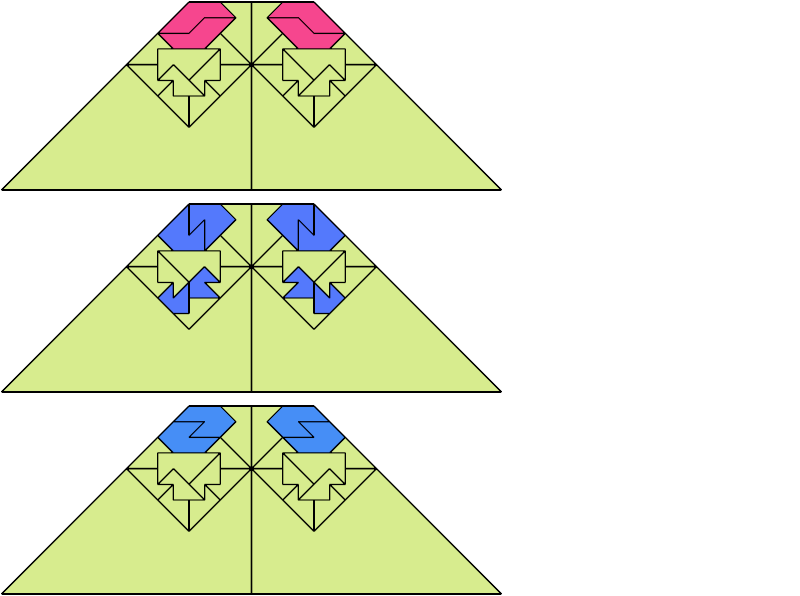
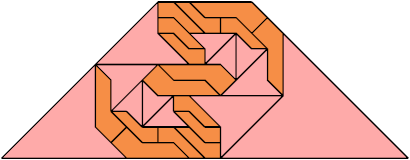
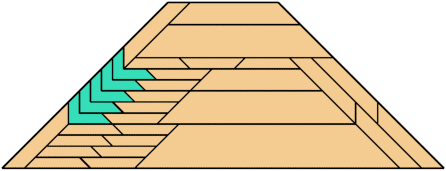
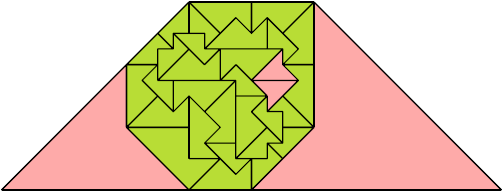
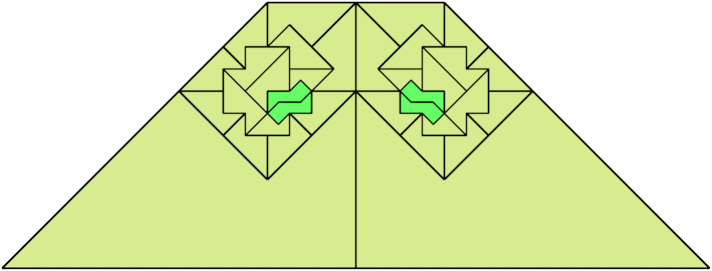
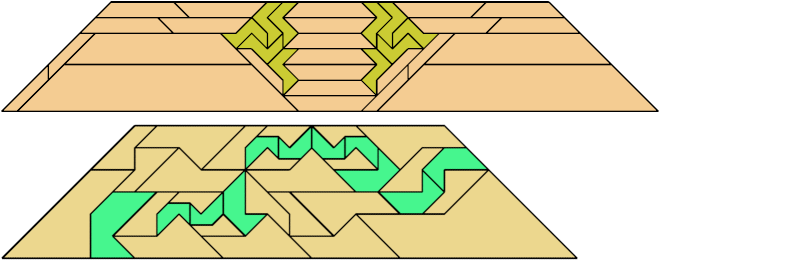
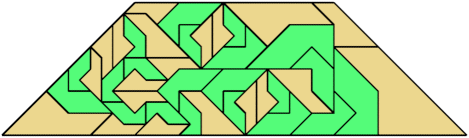
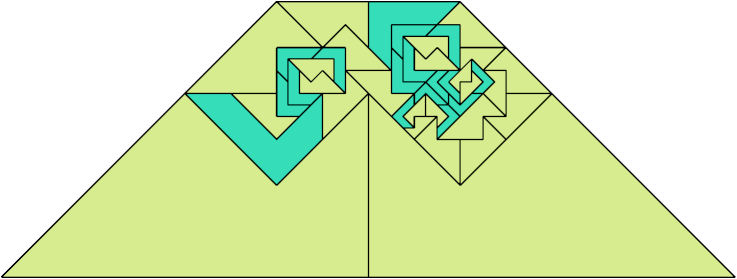
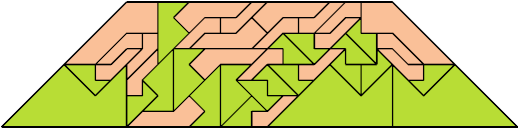
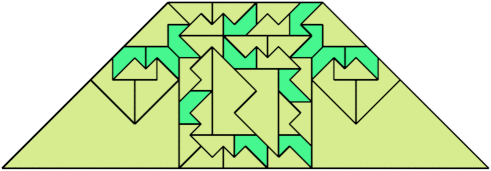
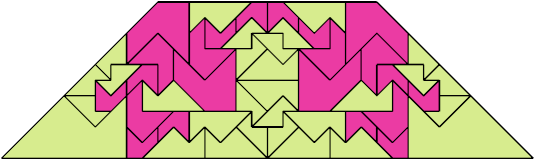
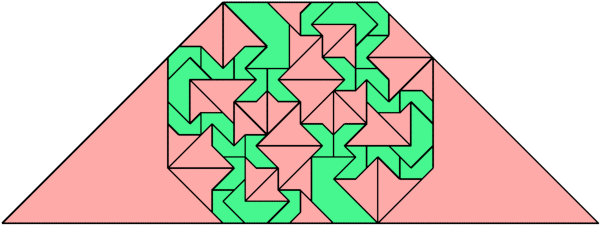
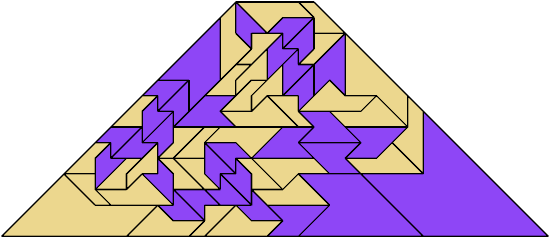
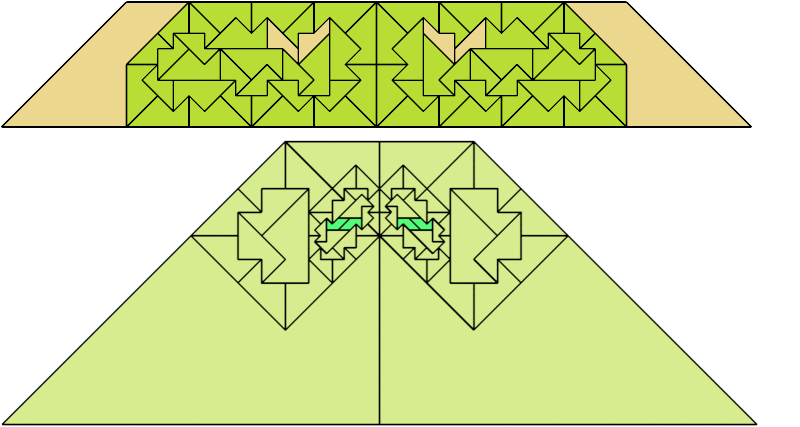
For every pair of scaled pentaboloes, I show an isosceles trapezium that they can tile, using at least one of each, and using as few tiles as known to be possible. If you find a smaller solution or solve an unsolved case, please write.

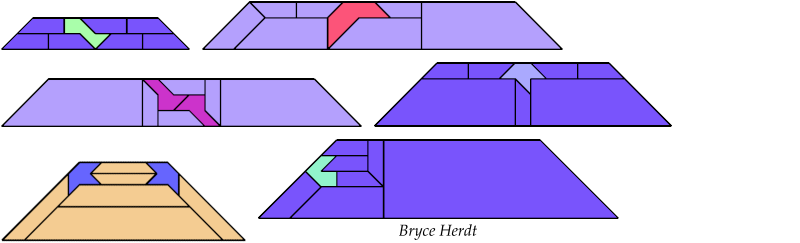
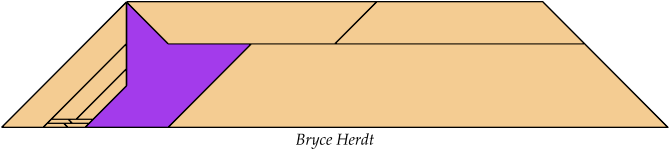
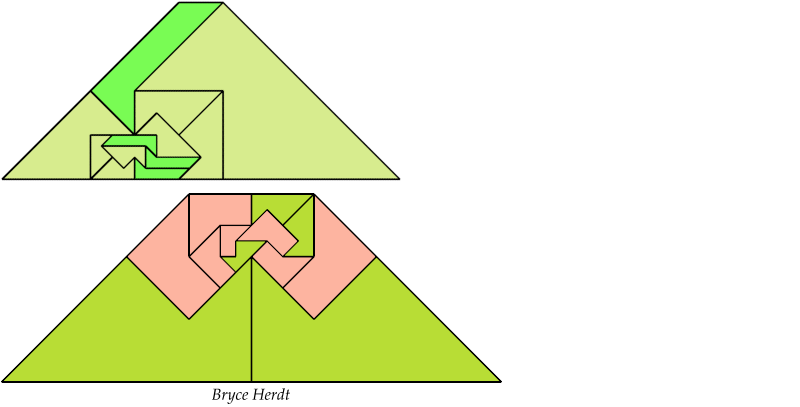
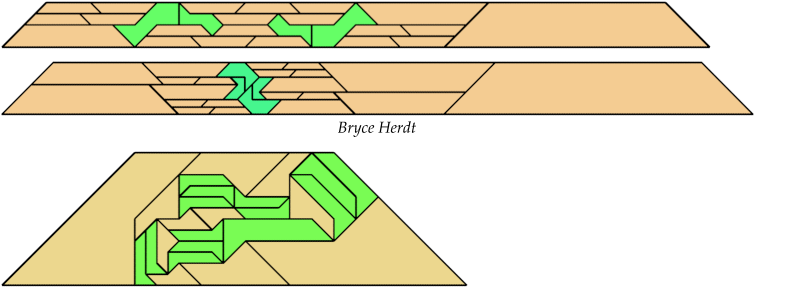
Bryce Herdt found improved solutions.

See also

• Tiling Right Trapezia with Scaled Pentabolo Pairs

Table of Results

Theoretically, scaled pentabolo 24 and any other scaled pentabolo can together tile an isosceles trapezium. I do not have tilings for all such pairs of scaled pentaboloes.

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30
2	?	•	?	?	?	?	?	5	4	?	?	?	4	?	?	?	?	?	?	?	?	?	?	26	?	?	3	?	?	7
8	18	5	?	?	?	36	?	•	4	?	20	4	?	?	4	?	3	?	?	?	14	?	?	?	?	79	4	4	7	?
9	8	4	7	6	8	5	7	4	•	8	7	7	6	6	5	6	8	5	6	8	4	7	6	4	6	4	3	4	5	3
24	?	26	52	3	?	23	?	?	4	?	26	26	?	?	4	42	23	45	66	34	12	?	?	•	?	66	14	43	12	33
26	?	?	14	?	?	6	?	79	4	?	6	?	4	?	7	?	?	35	41	?	25	?	?	66	?	•	5	?	?	?
27	5	3	7	21	14	18	11	4	3	8	7	7	9	37	7	32	23	25	21	25	4	15	16	14	35	5	•	7	5	7
30	9	7	24	7	?	7	?	?	3	?	7	7	?	?	3	21	?	64	16	?	22	?	?	33	?	?	7	28	?	•

Navigation

3 Tiles

4 Tiles

5 Tiles

6 Tiles

7 Tiles

8 Tiles

9 Tiles

11 Tiles

12 Tiles

14 Tiles

15 Tiles

16 Tiles

18 Tiles

20 Tiles

21 Tiles

22 Tiles

23 Tiles

24 Tiles

25 Tiles

26 Tiles

28 Tiles

32 Tiles

33 Tiles

34 Tiles

35 Tiles

36 Tiles

37 Tiles

41 Tiles

42 Tiles

43 Tiles

45 Tiles

52 Tiles

64 Tiles

66 Tiles

79 Tiles

Last revised 2025-10-13.