 |
 |
 |
 |
 |
Order-5 minimal solution |
All basic solutions for minimum sum prime number magic stars. |
Order-5 consecutive primes |
All basic solutions for consecutive prime number magic stars. |
Order-6 minimal solution |
All basic solutions for minimum sum prime number magic stars. |
Order-6 consecutive primes |
All basic solutions for consecutive prime number magic stars. |
Pcomp |
A magic star pair where the peaks of 1 are the others valleys . |
A Standard is Needed |
Why a standard is required for work with magic stars. |
Prime Magic Stars - 2 |
A page with Orders 7 & 8, patterns A & B, prime magic stars. |
![]()
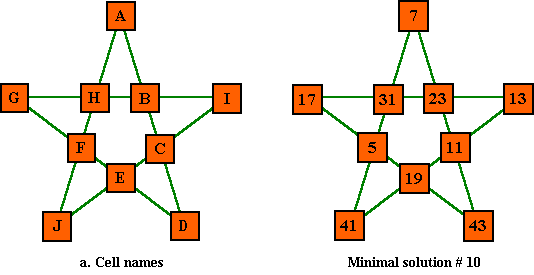
It is possible to construct a magic order-5 star using prime numbers. The minimal solution uses the following 10 prime numbers : 5, 7, 11, 13, 17, 19, 23, 31, 41, 43. Note that the primes 3, 29 and 37 are missing from this series. The only even prime number, 2, of course cannot be included because of parity.
The sum of the above prime series is 210 and the magic sum is 84 (S = 210 * 2/5).
The smaller series of primes from 3 to 41, again leaving out the 29 and 37, is a candidate because the sum is also evenly divisible by 5. However, there are not enough suitable combinations of 4 numbers summing to the constant 68 to permit construction of a magic star.
There are 12 basic solutions using the above set of prime numbers. Because each solution has 4 rotations and 5 reflections, there are 120 apparently different solutions. These basic solutions were first reported by Vasiliy Danilov on August 3, 1998 to Carlos Rivera in response to a puzzle posted on his Prime Puzzles web page at http://www.primepuzzles.net.
The 12 basic solutions are (in index order): Primes used are 5, 7, 11, 13, 17, 19, 23, 31, 41, 43
# A b c D e f G h I J sum Pcomp 1 . 5 7 31 41 13 19 11 43 23 17 84 9 2 . 5 7 41 31 13 17 23 43 11 19 84 10 3 . 5 17 19 43 11 7 23 31 13 41 84 8 4 . 5 17 43 19 11 41 13 31 23 7 84 11 5 . 5 19 17 43 23 7 11 41 13 31 84 7 reported by Rivera & 6 . 5 19 43 17 23 31 13 41 11 7 84 12 Ayala 7 . 7 5 31 41 13 11 19 43 17 23 84 5 8 . 7 5 41 31 13 23 17 43 19 11 84 3 9 . 7 11 23 43 17 5 19 41 13 31 84 1 10 . 7 23 11 43 19 5 17 31 13 41 84 2 reported by Vasiliy 11 . 11 13 19 41 5 7 31 23 17 43 84 4 12 . 19 13 11 41 7 5 31 17 23 43 84 6
As noted above, the basic solutions come in Pcomp (peak complement?) pairs, which can be transformed from one to the other by the following exchange routine. This moves the numbers at the peaks to the valleys, and the numbers in the valleys to the peaks.
Position A and E change places.
B moves to I, C moves to J,
d moves to C, F
moves to D
G moves to B, h moves to G,
I moves to H, J
moves to F
After these changes have been made, an additional step is required to convert from an equivalent solution to the new basic solution. This is called normalizing, and involves rotating one or more positions, and possibly reflecting the pattern as well, so the above conditions for a basic solution are met. I call these pairs Pcomp to differentiate from complement as it is normally used when dealing with pure magic squares and pure magic stars.
Vasiliy has a different routine for accomplishing this, but after normalizing, the end result is the same basic solution pair. Note that these pair members may be called compliments of each other. However, this is different to the compliment referred to in normal magic stars (or magic squares) where the compliment is obtained by subtracting each number from the sum of the first and last primes in the series used.. The result is sometimes, but not always, the same as using an exchange procedure like the above.
Note that like all magic squares and magic stars, prime magic stars may also be complemented (the conventional way) to produce another magic star. However, the complement of many of the prime numbers will not be a prime, so the result is only an impure magic star.
![]()
Prime series used: 3, 5, 7, 11, 13, 29, 31, 41, 47, 53 (primes 3 to 53 with no 17,19,23,37)
| # | A | b | c | D | e | f | G | h | I | J | sum | pcomp |
| 13 | 3 | 5 | 41 | 47 | 13 | 29 | 7 | 53 | 31 | 11 | 96 | 21 |
| 14 | 3 | 5 | 47 | 41 | 13 | 11 | 31 | 53 | 7 | 29 | 96 | 22 |
| 15 | 3 | 11 | 29 | 53 | 7 | 5 | 31 | 41 | 13 | 47 | 96 | 20 |
| 16 | 3 | 11 | 53 | 29 | 7 | 47 | 13 | 41 | 31 | 5 | 96 | 23 |
| 17 | 3 | 29 | 11 | 53 | 31 | 5 | 7 | 47 | 13 | 41 | 96 | 19 |
| 18 | 3 | 29 | 53 | 11 | 31 | 41 | 13 | 47 | 7 | 5 | 96 | 24 |
| 19 | 5 | 3 | 41 | 47 | 13 | 7 | 29 | 53 | 11 | 31 | 96 | 17 |
| 20 | 5 | 3 | 47 | 41 | 13 | 31 | 11 | 53 | 29 | 7 | 96 | 15 |
| 21 | 5 | 7 | 31 | 53 | 11 | 3 | 29 | 47 | 13 | 41 | 96 | 13 |
| 22 | 5 | 31 | 7 | 53 | 29 | 3 | 11 | 41 | 13 | 47 | 96 | 14 |
| 23 | 7 | 13 | 29 | 47 | 3 | 5 | 41 | 31 | 11 | 53 | 96 | 16 |
| 24 | 29 | 11 | 3 | 53 | 5 | 7 | 31 | 13 | 41 | 47 | 96 | 18 |
![]()
Prime series used: 7, 11, 13, 17, 19, 23, 29, 31, 43, 47 (primes 7 to 47 with no 3, 5, or 37)
| # | A | b | c | D | e | f | G | h | I | J | sum | pcomp |
| 25 | 7 | 11 | 31 | 47 | 13 | 17 | 19 | 43 | 23 | 29 | 96 | 33 |
| 26 | 7 | 11 | 47 | 31 | 13 | 29 | 23 | 43 | 19 | 17 | 96 | 34 |
| 27 | 7 | 17 | 29 | 43 | 23 | 11 | 19 | 47 | 13 | 31 | 96 | 31 |
| 28 | 7 | 17 | 43 | 29 | 23 | 31 | 13 | 47 | 19 | 11 | 96 | 35 |
| 29 | 7 | 29 | 17 | 43 | 19 | 11 | 23 | 31 | 13 | 47 | 96 | 32 |
| 30 | 7 | 29 | 43 | 17 | 19 | 47 | 13 | 31 | 23 | 11 | 96 | 36 |
| 31 | 11 | 7 | 31 | 47 | 13 | 19 | 17 | 43 | 29 | 23 | 96 | 27 |
| 32 | 11 | 7 | 47 | 31 | 13 | 23 | 29 | 43 | 17 | 19 | 96 | 29 |
| 33 | 11 | 19 | 23 | 43 | 29 | 7 | 17 | 47 | 13 | 31 | 96 | 25 |
| 34 | 11 | 23 | 19 | 43 | 17 | 7 | 29 | 31 | 13 | 47 | 96 | 26 |
| 35 | 17 | 13 | 19 | 47 | 11 | 7 | 31 | 29 | 23 | 43 | 96 | 28 |
| 36 | 19 | 13 | 17 | 47 | 7 | 11 | 31 | 23 | 29 | 43 | 96 | 30 |
Note that one of these three series of 12 solutions starts with the prime number 3, one
with prime 5, and one with prime 7.
There is another set of 12 solutions using primes 5, 7, 13, 19, 23, 29, 37, 41, 43, 53
with S = 108.
There is another set of 12 solutions using primes 5, 11, 13, 29, 31, 37, 41, 43, 47, 53
with S = 124.
There is another set of 12 solutions using primes 5, 13,17, 23, 31, 37, 41, 43, 47,
53 with S = 124.
Therefore there are a total of 72 distinct solutions using 10 of the 15 primes from 3 to
53.
The lowest possible Magic Pentagram using consecutive primes
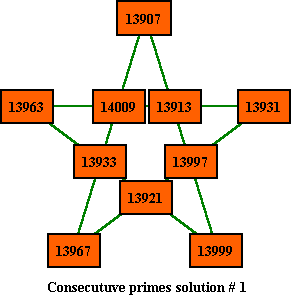 |
There are also 12 basic solutions to the order-5 consecutive primes magic star. This time the first set that works starts with the 1644th prime. The series of 10 consecutive primes start with 13907 and ends with 14009. It is worth noting that there are also 12 basic solutions to the minimal solution Prime Number Order-5 magic stars (above section). There are also 12 basic solutions to the minimal solution Order-5 magic stars.
|
# A b c D e f G h I J Sum Pcomp 1 13907 13913 13997 13999 13921 13933 13963 14009 13931 13967 55816 10 2 13907 13913 13999 13997 13921 13967 13931 14009 13963 13933 55816 9 3 13907 13933 13967 14009 13931 13913 13963 13999 13921 13997 55816 7 4 13907 13933 14009 13967 13931 13997 13921 13999 13963 13913 55816 11 5 13907 13967 13933 14009 13963 13913 13931 13997 13921 13999 55816 8 6 13907 13967 14009 13933 13963 13999 13921 13997 13931 13913 55816 12 7 13913 13907 13997 13999 13921 13963 13933 14009 13967 13931 55816 3 8 13913 13907 13999 13997 13921 13931 13967 14009 13933 13963 55816 5 9 13913 13931 13963 14009 13933 13907 13967 13997 13921 13999 55816 2 10 13913 13963 13931 14009 13967 13907 13933 13999 13921 13997 55816 1 11 13931 13921 13967 13997 13907 13913 13999 13963 13933 14009 55816 4 12 13963 13921 13933 13999 13907 13913 13997 13931 13967 14009 55816 6
Carlos Rivera and Jaime Ayala's solution to this part of their puzzle was:
a = 13907, b = 13921, c = 13913, d = 13933, e = 13931, f = 13963, w = 13999, x = 13997, y
= 13967,
z = 14009. When changed to my notation and normalized, it is the same as my index # 5.
Sample solutions from other consecutive prime sets
1 of 12 solutions using 10 consecutive primes starting at 23497
23497 23537 23563 23567 23509 23549 23539 23557 23531 23561 94164
1 of 12 solutions using 10 consecutive primes starting at 23831
23831 23869 23893 23899 23833 23873 23887 23879 23857 23909 95492
1 of 12 solutions using 10 consecutive primes starting at 29423
29423 29429 29501 29527 29443 29473 29437 29531 29483 29453 117880
There are 12 solutions for each series starting with 37447, 39313, 40813, 81331, 105361, 112207, 115303, 122453, etc.
![]()
Minimal solution Order-6 prime magic star using non-consecutive primes
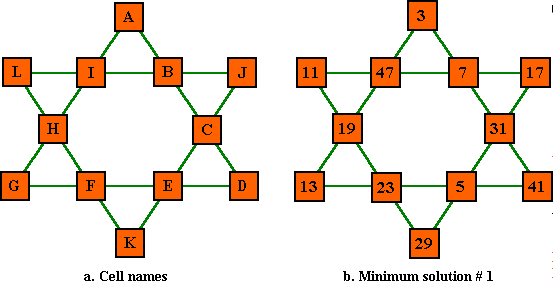
Primes used: 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 41, 47 These are all the basic solutions.
# A b c D e f G h i J K L sum type 1.. 3 7 31 41 5 23 13 19 47 17 29 11 82 1a see notes (below) 2.. 3 7 31 41 17 11 13 19 47 5 29 23 82 2a re Suzuki types 3.. 3 13 19 47 11 17 7 31 41 23 29 5 82 1b 4.. 3 13 19 47 23 5 7 31 41 11 29 17 82 2b 5.. 5 23 13 41 3 7 31 17 29 19 47 11 82 1c 6.. 5 23 47 7 3 41 31 17 29 19 13 11 82 2d too bad 2c & 2d 7.. 7 3 41 31 5 29 17 11 47 13 23 19 82 1d are not reversed! 8..17 11 13 41 3 7 31 5 29 19 47 23 82 2c
None of these 8 solutions can be converted so peaks and valleys are swapped (i.e. no
pcomp pairs).
Remember, when converting Suzuki types, you must rotate and/or reflect the pattern to
obtain the new basic solution.
Other almost minimal solutions
Primes used: 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 41, 53 These are all the basic solutions
1 .. 3 5 23 53 13 7 11 41 29 31 17 19 84 1a 2 .. 3 11 41 29 19 31 5 23 53 7 17 13 84 1b 3 .. 5 3 53 23 13 17 31 19 29 11 7 41 84 1c 4 ..13 7 11 53 3 5 23 31 17 41 29 19 84 1d
Primes used: 3, 5, 7, 11, 13, 17, 19, 23, 29, 37, 47, 59 These are all the basic solutions
1 .. 3 5 23 59 13 7 11 47 29 37 17 19 90 1a 2 .. 3 11 47 29 19 37 5 23 59 7 17 13 90 1b 3 .. 5 3 59 23 13 17 37 19 29 11 7 47 90 1d 4 .. 3 7 11 59 3 5 23 37 17 47 29 19 90 1c
Primes used: 3, 5, 7, 11, 13, 17, 19, 23, 29, 41, 43, 59 These are all the basic solutions
1 .. 3 5 59 23 7 19 41 17 29 13 11 43 90 1a 2 .. 3 23 59 5 13 43 29 17 41 7 11 19 90 1b 3 .. 5 3 23 59 7 11 13 43 29 41 19 17 90 1d 4 .. 7 11 13 59 5 3 23 41 19 43 29 17 90 1c
NOTES
Type refers to Suzuki groups. The number is the index number of A. B, C & D are
transformations of A.
See my Magic Stars Order-6 page for a full explanation of Suzuki
groups and Complement pairs.
It appears there are always a multiple of 4 basic solutions for order-6 magic stars,
because all may bedivided into Suzuki sets.
Pcomp refers to the opposite member of the pair which has the peaks and valleys reversed. I use the term Pcomp to differentiate from the term complement as it is normally used when dealing with pure magic squares and pure magic stars.
Not all solutions of order-6 prime number magic stars are members of pairs (unlike all pure magic stars). This is probably because any magic hexagon requires that the set of 12 numbers be capable of dividing into 2 sets of six numbers with the same sums, and 3 sets of four numbers with the same sums. Furthermore, in the case of prime numbers (or other non-consecutive number sets),each of the sets of 6 must be formed of 2 sets of three numbers with the same sum. Most of the prime sets cannot be arranged this way. Of those that can, most have not the correct values to permit six lines with the same sum.
In the case of the above low prime number series, there are no Pcomp pairs.
![]()
Solutions for Order-6 using consecutive primes 29-73
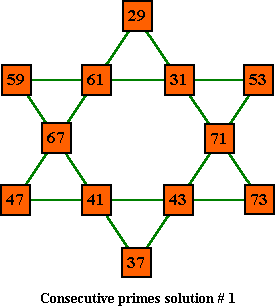 |
This is the smallest series of consecutive primes that can make an
order-6 magic star. Most of these solutions do not come in pcomp pairs, unlike all pure magic stars, and all the solutions for the order-5 prime number magic star.
|
# A b c D e f G h i J K L sum type Pcomp 1.. 29 31 71 73 43 41 47 67 61 53 37 59 204 1a 2.. 29 37 71 67 31 47 59 43 73 41 61 53 204 2a 3.. 29 37 71 67 41 53 43 73 59 61 31 47 204 3a 16 4.. 29 37 71 67 43 53 41 73 61 59 31 47 204 4a 15 5.. 29 41 73 61 47 59 37 71 67 53 31 43 204 4b 17 6.. 29 43 73 59 47 61 37 71 67 53 31 41 204 3b 19 7.. 29 47 61 67 41 37 59 43 73 31 71 53 204 5a 8.. 29 47 67 61 59 53 31 71 73 41 37 43 204 1b 9.. 29 59 43 73 53 31 47 61 67 37 71 41 204 5b 10.. 29 59 43 73 53 41 37 71 67 47 61 31 204 2b 11.. 31 29 73 71 43 37 53 59 61 47 41 67 204 1d 12.. 31 47 59 67 29 37 71 41 61 43 73 53 204 2c 13.. 31 53 73 47 29 67 61 41 71 43 59 37 204 5d 14.. 37 29 67 71 31 61 41 53 73 59 47 43 204 2d 15.. 37 29 67 71 41 31 61 47 59 43 53 73 204 3d 4 16.. 37 29 67 71 43 31 59 47 61 41 53 73 204 4d 3 17.. 41 31 61 71 37 29 67 43 53 47 59 73 204 3c 5 18.. 41 37 59 67 29 47 61 31 71 43 73 53 204 5c 19.. 43 31 59 71 37 29 67 41 53 47 61 73 204 4c 6 20.. 43 37 53 71 31 29 73 47 41 59 61 67 204 1c
The following solutions use consecutive primes 53 to 103 # A b c D e f G h i J K L sum type Pcomp 1..53 61 97 101 67 71 73 103 83 89 59 79 312 1a 6 2..53 61 97 101 73 71 67 103 89 83 59 79 312 2a 5 3..53 67 103 89 79 83 61 97 101 71 59 73 312 2b 7 4..53 73 103 83 79 89 61 97 101 71 59 67 312 1b 8 5..61 53 101 97 67 59 89 79 83 73 71 103 312 1d 2 6..61 53 101 97 73 59 83 79 89 67 71 103 312 2d 1 7..67 59 89 97 61 53 101 73 71 79 83 103 312 1c 3 8..73 59 83 97 61 53 101 67 71 79 89 103 312 2c 4 This is the only set for order-6 that I have found where all the solutions are in pairs. See above section for my definition for Pcomp.
The following solutions use consecutive primes from 59 to 107 # A b c D e f G h i J K L sum type Pcomp 1.. 59 61 103 107 67 83 73 97 101 89 71 79 330 1a 2..59 61 103 107 71 79 73 101 97 89 67 83 330 2a 3..59 67 97 107 61 73 89 103 79 101 71 83 330 3a 4..59 67 97 107 61 83 79 103 89 101 71 73 330 4a 5..59 73 97 101 79 89 61 103 107 83 71 67 330 1b 6..59 73 101 97 83 89 61 103 107 79 67 71 330 2b 7..59 79 103 89 73 101 67 97 107 83 71 61 330 4b 8..59 89 103 79 83 101 67 97 107 73 71 61 330 3b 16 9..61 59 107 103 67 71 89 79 101 73 83 97 330 1d 10..61 59 107 103 71 67 89 83 97 73 79 101 330 2d 11..61 71 101 97 67 59 107 79 83 73 89 103 330 4c 12..61 71 101 97 67 59 107 89 73 83 79 103 330 3c 13..67 59 107 97 61 71 101 73 89 79 83 103 330 4d 14..67 59 107 97 61 71 101 83 79 89 73 103 330 3d 15..67 71 89 103 61 59 107 73 83 79 101 97 330 1c 16..71 67 89 103 61 59 107 73 79 83 97 101 330 2c 8 Others solution sets start with 127 (8), 137 (16), 409 (12), 541 (12)
![]()
Introduction
In early summer of 1998, Carlos Rivera posted a two part puzzle on his Prime Puzzles & Problems web page (at http://www.primepuzzles.net)
When Carlos posted the puzzle he and his friend Jaime Ayala already had 10 solutions for part A and 1 solution for part B of the puzzle.
On August 3/98 Vasiliy Danilov sent Carlos six solutions for part A. of the puzzle, and explained how they could be transformed to 12 solutions.
Subsequently, I also worked on this puzzle.
The end result was three sets of solutions with three different notations. Here I
compare them and make some suggestions for a standard.
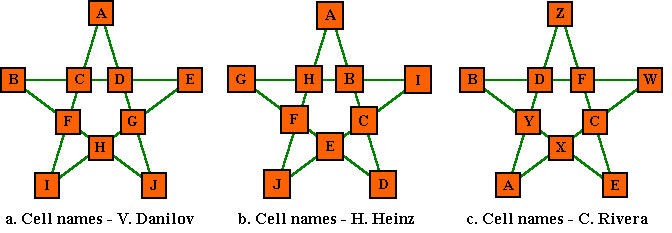
Puzzle part A -- Minimal Sum Prime Number Magic Star
Example a.
Vasiliy Danilov:
a = 43, b = 13, c = 11, d = 19, e = 41, f = 23, g = 5, h = 31, i = 7, j = 17
Harvey Heinz (solution # 10)
a = 7, b = 23, c = 11, d = 43, e = 19, f = 5, g = 17, h = 31, i = 13, j = 41
These solutions are equivalent, but obviously they do not look like it, and it is impossible to compare them without actually drawing the star and assigning the values to the correct cells, as per the left and middle diagrams above.
When this is done, they are still not identical, but are only apparently different. One may be called a basic solution, the other an equivalent solution. Equivalent solutions are rotations and/or reflections of the basic solution. As there are 2 reflections and 5 rotations for the order-5 magic star, there are 10 apparently different solutions, of which only one is called the basic solution. In general, for any order n magic star, there are 2n-1 apparently different solutions for each basic solution.
The question now is, which solution do we call the basic solution?
I propose the following:
To qualify as a basic solution, two conditions are required:
We now see that by this definition, mine is the basic solution and Vasiliy's solution is an equivalent one. It must be rotated right (clockwise) two positions to become the basic solution. This process is referred to as normalization.
Example b.
Carlos Rivera & Jaime Ayala (1 of 10 solutions found)
a = 5, b = 11, c = 17, d = 7, e = 13, f = 23, w = 43, x = 19, y = 41, z = 31
Harvey Heinz (solution # 5)
a = 5, b = 19, c = 17, d = 43, e = 23, f = 7, g = 11, h = 41, i = 13, j = 31
For this example, assign the values to the stars as per the two layouts (middle and right, above). By the above definition, my solution is the basic one, Carlos & Jaime's is an equivalent solution. Change it to the basic solution by rotating right (clockwise) 3 positions. In this case the normalization is complete only after a reflection of the pattern is made.
We now have a definition for what constitutes a basic solution, except no mention was made regarding the order of recording the values.
I propose the values be assigned and recorded by tracing out the lines of the star as per the middle diagram (Heinz) above. Quite often you see these values presented horizontal line by line (Danilov). This is acceptable for Order-5 or 6 magic stars but becomes hopelessly confusing when higher order stars are considered.
Having a standard definition for what is a basic solution makes it possible for different investigators to compare their lists of basic solutions for a given order of magic star.
1. All solutions have a unique index number.
2. After normalization, it is immediately apparent if two solutions are equivalent
because, after sorting,
they will be identical and appear
adjacent in the list.
3. It is not necessary for comparison purposes, to actually draw the diagram
and assign the values to it.
Please refer to my Magic Stars Definitions page
for more detail.
Please refer to my Magic Stars -2 page
for similar information on order 7 and 8 prime magic stars.
Please send me Feedback about my Web
site!![]()
![]()

![]()
Harvey Heinz harveyheinz@shaw.ca
Last updated March 01, 2005
Copyright © 1998, 2000, 2001 by Harvey D. Heinz