 |
 |
 |
 |
 |
Andrew Howroyd has been investigating magic
stars.
Here I share with you the information he sent me via email.
![]()
Email of Feb. 24, 2005 I have reformatted this slightly for improved clarity.
I have some information on magic stars that you
might be interested in.
I enjoyed looking at your web site.
NUMBER OF SOLUTIONS
The following are the number of magic stars for orders from 10 to 13. My figures
agree with yours for orders 6 to 11 inclusive. The counting was done by computer
using a brute force approach with some optimizations. I have tried a couple of
different algorithms and consistently come to the same results, and given that
they also agree with yours that indicates a good chance of correctness.
If you would like a copy of the program I can send it to you (Java).
10a: 10,882 (0.5 seconds)
10b: 115,552 [=16 * 7,222] (19 seconds)
10c: 10,882 (=10a)
11a: 53,528 (4 seconds)
11b: 75,940 (3 minutes)
11c: 53,528 (=11c)
11d: 75,940 (=11d)
12a: 396,930 (29 seconds)
12b: 826,112 [=2 * 413,056] (16 minutes)
12c: 560,348 [=2 * 280,174] (7 minutes)
12d: 496,336 (6 minutes)
13a: 2,434,692 (4 minutes)
13b: 3,044,940 [=2 * 1,522,470] (4 hours)
13c: 3,510,442 (2 hours)
13d: 2,434,692 (=13a)
13e: 3,510,442 (=13c)
WHEN ARE COUNTS THE SAME
-------------------------------------------------
The following list shows which pairs of star type have a 1-1 relation between them. This list is complete up to order 20 and has also been verified by computer search.
7b ~ 7a
8b ~ 8a alt
9c ~ 9b alt
10c ~ 10a
11c ~ 11a alt
11d ~ 11b
13d ~ 13a
13e ~ 13c alt
14d ~ 14a alt
14e ~ 14b alt
15f ~ 15c
16d ~ 16c alt
16e ~ 16a
16f ~ 16b
17c ~ 17b
17e ~ 17a alt
17g ~ 17d alt
18c ~ 18b alt
18f ~ 18e alt
19e ~ 19c
19f ~ 19a
19g ~ 19b alt
19h ~ 19d
20f ~ 20a alt
20h ~ 20c alt
Some points of interest:
All of the order 12-types are different - there are no pairs at all. Some other orders (15, 18, 20) have fewer than the full complement of pairs. Notably these orders are neither prime nor twice a prime.
The transformations between two types of the same order can be divided into two groups. Firstly there are those like 8b <-> 8a. Here the outside points are swapped with the valley points. Other transformations like 10c <-> 10a keep outside points as outside points.
Formulas:
The following is a formula to test if two types are paired.
Calculate 2 * step1 * step2 - step1 - step2
where step1 is the step between points of the first type (i.e. 2 for type 11a, 3 for 11b, 4 for 11c, 5 for 11d etc) and step2 is the step between points of another type to test.
Both step1 and step2 are between 2 and half the order.
Then divide the result by the number of points keeping only the remainder.
If the remainder is zero then the two stars are paired as in 10c <-> 10a.
If the remainder is one less than the order then the two stars are paired as in
8b <-> 8a
Otherwise there is no pairing relation.
Example 1: To test if type 11b and 11d are paired
Calculate 2 * 3 * 5 - 3 - 5 = 30 - 8 = 22 = 2 * 11 exactly, so the two are paired
Example 2: To test if type 8a and 8b are paired
Calculate 2 * 2 * 3 - 2 - 3 = 12 - 5 = 7 = 8 - 1, so the two are also paired
Algorithm:
Pick any row on the star to be transformed. If the points are A,B,C,D rearrange them to be A,C,B,D (if outside points remain outside points) or B,D,A,C (if outside points are swapped with valley points) and place the line anywhere on the target star. Now pick another line that crosses the first line at any point and transform the points as before and place the line in the only position allowed. Continue in this manner until the whole star has been transformed.
PERMUTATIONS
--------------------
Some star types can be re-arranged other than by simple rotation / reflection to give new stars. For example, all 80 type 6 stars can be obtained from a core set of 20. Permutations do not, however, exist for all star types - in fact they are fairly rare. The main group is the sequence 6a, 10b, 14c, 18d.... The following table shows the star type vs. the number of permutations.
Type 6a 4
Type 10b 16
Type 14c 64
Type 18d 256
The number of permutations is given by the formula: 2^(2k) where the order of the star is 4k + 2 and k is the step between outside points (a=2, b=3...).
The permutation works by swapping 4 pairs of points
I have edited order-10-1b to illustrate how the transform works. (see attachment). The 4 pairs of coloured squares are exchanged. It is easy to visually see that the two vertical lines are swapped over in their entirety so the sum is not affected. All lines that pass through the two vertical lines keep the same elements. By applying the one transform at different rotations, all the possible permutations can be obtained.
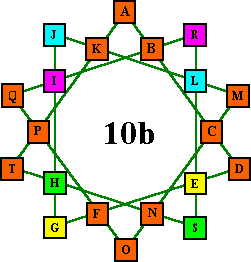
The fact that Type 10b has a permutation count of 16 explains why there are so many more 10b stars compared with 10c/10a. If numbers of permutations are factored out then the number of stars appears to increase strictly with the number of points. There are really only 20 primitive type 4 stars which is less than the number of type 7 stars (72). Similarly, if each of the 16 type 10b stars is only counted as one then the total number of type 10 stars will come in as less than the number of type 11 stars.
Others
Other special permutations also exist for some star types.
In particular if 2 * k * k - 2k is an exact multiple of the order or one less where k is the step between outside points.
Type 12b 2
Type 12c 2
Type 13b 2
Type 15e 2
Type 17f 2
Type 20d 2
Type 20e 2
To perform the transform just use the same procedure as for transforming a star from one type to another.
There are no other general purpose transforms for orders up to 20.
Order10-1b.bmp (shown above) was attached to this email. I renamed the image because of a conflict.
![]()
Email of Feb. 26, 2005
Yes, please feel free to add my information to your web site in the way you feel best. I have absolutely no intention of starting my own web site!! Your web site is superb and is actually what got me onto exploring magic stars and squares in a bit of detail.
--- Some material deleted ---
When it comes to searching for solutions I have two separate algorithms. The one that is most interesting consists of the functions scangroup, scanblkalt and scanblkall (between lines about 700-1000). This is my second attempt: the code is quite flexible and is driven by tables that are set up in scanblkall (the main function). Because of the table driven approach, it would not be too difficult to adapt the code to other tasks.
The important ideas are:
1) the first stage (scanblkalt) searches for all solutions modulo some small number (say 5). This can be done pretty quickly as there are not too many solutions. The second stage (scangroup) then expands those into real solutions.
2) the zero is placed in a fixed position on the star. (I am numbering from zero upwards for coding simplicity). There are only two options: either it is an outside point or it is an inside point. This gives rise to a slightly different definition of a normal star than your. I always put the zero on the first outside point, or the valley point immediately to the right. In the later case, the first outside point is unlikely to be the least outside point. This optimisation reduces the search by one point - which is pretty significant.
3) the order in which points are resolved has a major influence on performance. This was the down-fall of my first attempt which uses a fixed order - one that works very well for the type 10a .. type 13a etc, but deteriates rapidly for the 'b' types and can't cope with higher steps at all. This is the motivation behind the table driven strategy.
The first part of the code in 'scanblkall' puts the order the points will be processed into the array 'm_ptindex'. I have one default strategy (which also only works well for small steps - because it is similar to my first attempt), but for the types 12c, 12d and 13c I have designed custom orders. These are just my first attempts and I have not tried other plausible alternatives. If you look at the definitions for ms_order12c, ms_order12d, ms_order13c it might initially appear that there is not much logic. (and may be there is not). In defining these tables the principals I have adopted are. a) Always fill out lines with only one remaining point, before lines with only two remaining points, before lines with three remaining points. That just seems to be common sense. b) Try to get around the star in a circle so as to create an intersection with the starting line as early as possible. (this strategy is only good for step sizes that are a large percentage of the number of points). In the case of 12c this is easy as 3 lines make a triangle. In the case of 12d, I drop back one point after each line to achieve the same thing. (you probably need to look at the point order and draw it out on a bit of paper or one of your diagrams to see what is going on). The only restriction on the point order is that point zero should be the first point and the second point should be a valley point (pref the one just to the right).
Once the point processing order is defined, the next bit of code sets up the control tables. (m_row1, m_row2 and m_action) and then the code jumps into the recursive function 'scanblkalt'. In turn once scanblkalt discovers a solution modulo the group count (a small number) it jumps into the recursive function 'scangroup'. When scangroup completes it increments a counter (m_count). There are some commented out bits of code here - this is where you would add something to do anything with the solutions. For example, isSolution() tests if the solutions is valid and saveSolution() adds the solution to an array for subsequent post-processing or saves the result to a file.
My first attempt at an algorithm occupies the functions scanloop to scanall (lines 1000 - 1300). The algorithm uses a fixed point order and does not employ the modulo trick - yet this is the code that produces the incredible times for types 12a and 13a - it's also the one for the 12b and 13b, but that seems to be about the cross over point. I have not yet spent the time to understand why this algorithm hugely out performs my new improved version on the 12a/13a types. (It should not do). The main differences are:
a) uses double linked list instead of single
linked list for tracking unused available values.
b) in main iterative loop processes two points at time.
c) has some optimization for early elimination of some solutions
d) always ensures the value to the left of the zero is lower than the one to right at the start. (This is to avoid counting reflections). Lines are processed counter clockwise so the one on right is completed last - it is noticeably faster to do that one last.
e) Calculates one point towards the end using formula instead of trying all possibilities. When I first added this optimization I was disappointed with the results - especially for the type 'a' solutions where there was only a marginal improvement.
As I say I have not yet determined which of the above reasons causes the old algorithm to out perform the smart one for the type 'a' problems. I suspect there is still room for improvement on the new algorithm, but sometimes it seems easier to wait a couple of hours for processing rather than spend a couple of days tweaking.... I am sure you have been there. Getting numbers for the 14's might not be straight forward - In particular, I suspect type 14c will have about 500 million solutions (given the x64 multiplier) - this could be avoided by only counting 1 in 64, but how?
I hope the above explanation goes some way to making up for a lack of comments.
Andrew
There were two attachments: Scanstar.jpx and ScanStar.java
![]()
This descriptive text appeared at the
start of the program listing in ScanStar.java.
Compare solution totals and search times with my results of circa 1995
here.
Results
Type 6a total 80 time 16ms
Type 7a total 72 time 0ms
Type 7b total 72 time 47ms
Type 8a total 112 time 15ms
Type 8b total 112 time 313ms
Type 9a total 3014 time 78ms
Type 9b total 1676 time 2469ms
Type 10a total 10882 time 515ms
Type 10b total 115552 time 18797ms
Type 11a total 53528 time 4547ms
Type 11b total 75940 time 160750ms
Type 12a total 396930 time 28500ms
Type 12b total 826112 time 983579ms
Type 12c total 560348 time 410656ms
Type 12d total 496336 time 395203ms
Type 13a total 2434692 time 241687ms
Type 13b total 3044940 time 14056563ms
Type 13c total 3510442 time 7758438ms
Type 12a total 396930/0 time 300235ms
Type 12b total 826112/0 time 2017593ms
Type 12c total 560348/0 time 4825485ms
// other algorithm
Type 10a total 10882/0 time 4313ms
Type 10b total 115552/0 time 19171ms
Type 11a total 53528/0 time 31032ms
Type 11b total 75940/0 time 162062ms
Type 12a total 396930/0 time 172938ms
Type 12b total 826112/0 time 1227078ms
This descriptive text appeared two-thirds of the way through the program listing in ScanStar.java.
// This block of code is used for enumerating and
counting solutions.
// scanall: top level function
// toploop: recursive function for first few points
// scanloop: main recursive function
// init: initialisation helper
// unlink, relink, setminmax: helpers for toploop
// Definitions:
// Rows, outside and valley points are numbered 0..n-1
// Valley point 0 lies between outside points 0 and 1.
// Row i contains outside point i and outside point i + m_delta
// Row i contains valley point i + 1 amd valley point i + m_delta - 1
// The algorithm proceeds as follows.
// 'init' sets up double linked list of available values. Value zero is
// left out since it is always used early on. Totals for each row are also
// initialised to the required row sum.
// 'toploop' sets up outside points 0..delta-1 inclusive and valley points
// 0..delta-2 inclusive. With delta == 2 that's a total of 3 points.
// Two scenarious are run: Either the zero value is a valley point or it
// is an outside point. For the first case, toploop puts the zero point in
// valley point 0, and flanks it with outside point 0 more than outside
// point 1. In the other case, the zero point is put on outside point 0 and
// then valley point n-1 is assigned only values more than valley point 0.
// The main loop is scanloop which processes two points at a time.
// Rows are processed in reverse order starting with row n-1.
// At each step two of the four points are already known and so it enough
// to assign all possible values to one and calculate the other.
// Once all but delta valley points and delta-1 outside points have been
// assigned, scanloop calculates the remainder.
![]()
Please send me Feedback about my Web
site!
![]()
![]()

![]()
Harvey Heinz harveyheinz@shaw.ca
This page last updated
March 01, 2005
Copyright © 2005 by Harvey D. Heinz